(本小题满分12分)在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,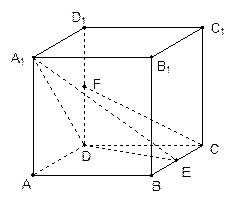
(1)求点A到平面A1DE的距离;
(2)求证:CF∥平面A1DE,
(3)求二面角E-A1D-A的平面角的余弦值。
若点M是 ABC所在平面内一点,且满足:
ABC所在平面内一点,且满足: .
.
(1)求 ABM与
ABM与 ABC的面积之比.
ABC的面积之比.
(2)若N为AB中点,AM与CN交于点O,设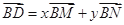 ,求
,求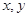 的值.
的值.
已知 ,且
,且 .
.
(1)求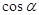 的值.
的值.
(2)若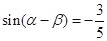 ,
, ,求
,求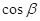 的值
的值
已知函数 .
.
(1)求 的最小正周期.
的最小正周期.
(2)若将 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 在区间
在区间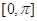 上的值域.
上的值域.
在已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为M(
,且图象上一个最低点为M(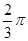 ,-2).
,-2).
(1)求f(x)的解析式;
(2)当x∈[ ,
, ]时,求f(x)的值域.
]时,求f(x)的值域.
已知f(x)=sin(-2x+ )+
)+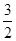 ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期和单调增区间.
(2)函数f(x)的图象可以由函数y=sin 2x(x∈R)的图象经过怎样的变换得到?