如图所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为,两侧为相同的匀强磁场,方向垂直纸面向里。一质量为、带电量、重力不计的带电粒子,以初速度垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动。已知粒子第二次在磁场中运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推。求

(1)粒子第一次经过电场的过程中电场力所做的功。
(2)粒子第次经过电场时电场强度的大小。
(3)粒子第次经过电场所用的时间
(4)假设粒子在磁场中运动时,电场区域场强为零。请画出从粒子第一次射入磁场至第三次离开电场的过程中,电场强度随时间变化的关系图线(不要求写出推导过程,不要求标明坐标刻度值)。
汽车先以a1=0.5m/s2的加速度由静止开始做匀加速直线运动,在20s末改做匀速直线运动,当匀速运动持续10s后,因遇到障碍汽车便紧急刹车,已知刹车的加速度为a2=-2m/s2,求:
(1)汽车匀速运动时的速度大小;
(2)汽车刹车后的6s内所通过的位移;
(3)在坐标图上画出该汽车运动全过程的v一t图象。
在5m高处以10m / s 的速度水平抛出一小球,不计空气阻力,g 取 10 m / s2,
求: (1)小球在空中运动的时间;
(2)小球落地时的水平位移大小;
(3)小球落地时的速度大小。
如图所示,实线为t1 = 0时刻的图象,虚线为t2 = 0.1s时刻的波形。
试求:
(1)若波的传播方向为+x方向,波速多大?
(2)若波的传播方向为-x方向,波速多大?
(3)若波速为450m/s,波沿什么方向传播?
某交流发电机输出功率为5×105 W,输出电压为1.0×103 V,已知输电线的总电阻R =" 40" Ω,在输电线上损失的电功率等于输电功率的5%,用户使用电压U="380" V.输电所使用的变压器均为理想变压器。
(1)画出输电线路的示意图.(标明各部分的符号)
(2)求所用升压和降压变压器的原、副线圈的匝数比各是多少?
如图所示,边长为 的单匝正方形线圈在磁感应强度为B的匀强磁场中,以
的单匝正方形线圈在磁感应强度为B的匀强磁场中,以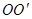 边为轴匀速转动,角速度为
边为轴匀速转动,角速度为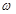 ,转轴与磁场方向垂直,线圈电阻为R。
,转轴与磁场方向垂直,线圈电阻为R。
求:
(1)线圈从图示位置转过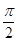 的过程中产生的热量Q。
的过程中产生的热量Q。
(2)线圈从图示位置转过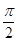 的过程中通过线圈某截面的电量
的过程中通过线圈某截面的电量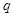 。
。