如图所示，空间有场强的竖直向下的匀强电场，长的不可伸长的轻绳一端固定于点，另一端系一质量的不带电小球，拉起小球至绳水平后，无初速释放．另一电荷量、质量与相同的小球，以速度水平抛出，经时间与小球在点迎面正碰并粘在一起成为小球，碰后瞬间断开轻绳，同时对小球C施加一恒力，此后小球与点下方一足够大的平板相遇．不计空气阻力，小球均可视为质点，取．
（1）求碰撞前瞬间小球的速度。
（2）若小球经过路到达平板，此时速度恰好为，求所加的恒力。
（3）若施加恒力后，保持平板垂直于纸面且与水平面的夹角不变，在点下方任意改变平板位置，小球均能与平板正碰，求出所有满足条件的恒力。
已知地球到太阳的距离约为1.5×1011m，万有引力常量为G=6.67×10-11N、m2/kg2。试由常识通过计算求：
（1）太阳的质量M（保留一位有效数字）;
（2）已知火星绕太阳做圆周运动的周期为1.9地球年，求地球与火星相邻两次距离最近时的时间间隔t。
把一个质量为0.5kg的小球，以20m/s的初速度竖直向上抛出，运动过程中小球始终受到水平方向大小恒为F=10N的风力的作用，g=10m/s2,求:
（1) 小球上升的最大高度H。
（2）小球在空中滞留的时间。
（3）小球落地点与抛出点之间的水平距离（设地面水平）。
如图所示装置中，区域I和Ⅲ中分别有竖直向上和水平向右的匀强电场，电场强度分别为E和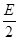
；Ⅱ区域内有垂直纸面向外的水平匀强磁场，磁感应强度为B。一质量为m、带电量为q的带负电粒子（不计重力）从左边界O点正上方的M点以速度V0水平射人电场，经水平分界线OP上的A点与OP成600角射入Ⅱ区域的磁场，并垂直竖直边界CD进入Ⅲ区域的匀强电场中。求：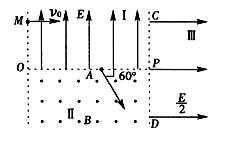
(1)粒子在Ⅱ区域匀强磁场中运动的轨道半径
(2)O、M间的距离
(3)粒子从M点出发到第二次通过CD边界所经历的时间
如图所示，在光滑绝缘的水平面内，对角线AC将边长为L的正方形分成ABC和ADC两个区域，ABC区域有垂直于水平面的匀强磁场，ADC区域有平行于DC并由C指向D的匀强电场．质量为m、带电量为+q的粒子从A点沿AB方向以v的速度射入磁场区域，从对角线AC的中点O进入电场区域．
（1）判断磁场的方向并求出磁感应强度B的大小．
（2）讨论电场强度E在不同取值时，带电粒子在电场中运动的时间t．
如图所示，质量为m的小球悬挂在长为L的细线下端，将它拉至与竖直方向成θ=60°的位置后自由释放．当小球摆至最低点时，恰好与水平面上原来静止的、质量为2m的木块相碰，碰后小球速度反向且动能是碰前动能的
．已知木块与地面的动摩擦因素μ=
，重力加速度取g．求：
（1）小球与木块碰前瞬间所受拉力大小
（2）木块在水平地面上滑行的距离