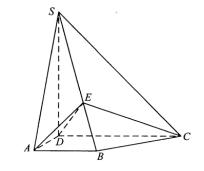
如图，四棱锥SABCD中，SD⊥底面ABCD，AB//DC,-优题课

题文

如图，四棱锥 $S - A B C D$ 中， $S D ⊥$ 底面 $A B C D$ ， $A B / / D C, A D ⊥ D C, A B = A D = 1, D C = S D = 2$ ， $E$ 为棱 $S B$ 上的一点，平面 $E D C ⊥$ 平面 $S B C$ .
（Ⅰ）证明： $S E = 2 E B$ ；
（Ⅱ）求二面角 $A - D E - C$ 的大小 .

科目数学题型解答题难度较难

登录免费查看答案和解析

相关试题

已知 $\{a_{n}\}$ 是以 $a$ 为首项， $q$ 为公比的等比数列， $S_{n}$ 为它的前 $n$ 项和．
（Ⅰ）当 $S_{1}$ 、 $S_{3}$ 、 $S_{4}$ 成等差数列时，求 $q$ 的值；
（Ⅱ）当 $S_{m}$ 、 $S_{n}$ 、 $S_{l}$ 成等差数列时，求证：对任意自然数 $k$ ， $a_{m + k}$ 、 $a_{n + k}$ 、 $a_{l + k}$ 也成等差数列．

如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $∠ B A C = 90^{°}$ ， $A B = A C = A A_{1} = 1$ ，延长 $A_{1} C_{1}$ 至点 $P$ ，使 $C_{1} P = A_{1} C_{1}$ ，连接 $A P$ 交棱 $C C_{1}$ 于 $D$ ．

（Ⅰ）求证： $P B_{1} / /$ 平面 $B D A_{1}$ ；
（Ⅱ）求二面角 $A - A_{1} D - B$ 的平面角的余弦值；

已知函数 $f \sin (x + \frac{7 π}{4}) + \cos (x - \frac{3 π}{4})$ ， $x \in R$ ．
（Ⅰ）求 $f (x)$ 的最小正周期和最小值；
（Ⅱ）已知 $\cos (β - α) = \frac{4}{5}, \cos (β + α) = - \frac{4}{5}, 0 < α < β < \frac{π}{2} .$ 求证： $[f {(β)}^{2}] - 2 = 0$ ．

本着健康、低碳的生活理念，租自行车骑游的人越来越多．某自行车租车点的收费标准是每车每次租车不超过两小时免费，超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算)．有甲、乙人互相独立来该租车点租车骑游（各租一车一次）．设甲、乙不超过两小时还车的概率分别为 $\frac{1}{4}$ 、 $\frac{1}{2}$ ；两小时以上且不超过三小时还车的概率分别为 $\frac{1}{2}$ 、 $\frac{1}{4}$ ；两人租车时间都不会超过四小时．
（Ⅰ）分别求出甲、乙在三小时以上且不超过四小时还车的概率；
（Ⅱ）求甲、乙两人所付的租车费用之和小于6元的概率．

（本小题满分12分）
设函数f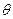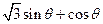（）=，其中，角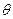的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P（x,y），且.
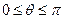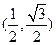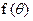（1）若点P的坐标为，求的值；
（II）若点P（x，y）为平面区域Ω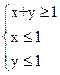：，上的一个动点，试确定角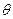的取值范围，并求函数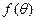的最小值和最大值.

试卷网试题网古诗词网作文网范文网