某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
| 规格类型 钢板规格 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
2 |
1 |
1 |
| 第二种钢板 |
1 |
2 |
3 |
今需A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需A、B、C三种规格成品,且使所用的钢板的张数最少?
已知等差数列{an}的前n项和为Sn,S5=35,a5和a7的等差中项为13.
(1)求an及Sn;
(2)令bn= (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn.
函数 .
.
(1)求函数f(x)的最小正周期;
(2)在△ABC中,a,b,c分别为内角A,B,C的对边,且 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.
定义在 上的函数
上的函数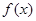 满足对任意
满足对任意 都有
都有 .
.
且 时,
时, ,
,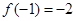
(1)求证: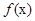 为奇函数;
为奇函数;
(2)试问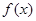 在
在 上是否有最值?若有,求出最值;若无,说明理由;
上是否有最值?若有,求出最值;若无,说明理由;
(3)若 对任意
对任意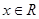 恒成立,求实数
恒成立,求实数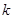 的取值范围.
的取值范围.
设 为实数,函数
为实数,函数 .
.
(1)若函数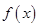 是偶函数,求实数
是偶函数,求实数 的值;
的值;
(2)若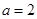 ,求函数
,求函数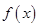 的最小值;
的最小值;
(3)对于函数 ,在定义域内给定区间
,在定义域内给定区间 ,如果存在
,如果存在 ,满足
,满足 ,则称函数
,则称函数 是区间
是区间 上的“平均值函数”,
上的“平均值函数”,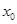 是它的一个“均值点”.如函数
是它的一个“均值点”.如函数 是
是 上的平均值函数,
上的平均值函数, 就是它的均值点.现有函数
就是它的均值点.现有函数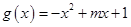 是区间
是区间 上的平均值函数,求实数
上的平均值函数,求实数 的取值范围.
的取值范围.