己知双曲线C: 与直线l:x + y = 1相交于两个不同的点A、B
与直线l:x + y = 1相交于两个不同的点A、B
(I) 求双曲线C的离心率e的取值范围;
(Ⅱ) 设直线l与y轴交点为P,且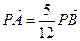 ,求
,求 的值。
的值。
已知函数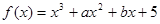 ,曲线
,曲线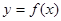 在点
在点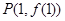 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)求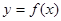 在
在 上的最大值.
上的最大值.
给定两个命题, :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :
: .如果
.如果 ∨
∨ 为真命题,
为真命题, ∧
∧ 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
在 中,角
中,角 所对边分别为
所对边分别为 ,已知
,已知 ,且最长边的边长为
,且最长边的边长为 .求:
.求:
(1)角 的正切值及其大小;
的正切值及其大小;
(2) 最短边的长.
最短边的长.
数列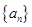 的前
的前 项和为
项和为 ,
, .
.
(1)求数列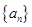 的通项公式;
的通项公式;
(2)设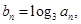 求数列
求数列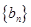 的前
的前 项和
项和 .
.
已知椭圆 、抛物线
、抛物线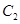 的焦点均在
的焦点均在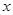 轴上,
轴上, 的中心和
的中心和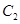 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录如下:
,从每条曲线上取两个点,将其坐标记录如下: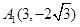 、
、 、
、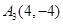 、
、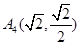 .
.
(1)经判断点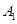 ,
,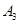 在抛物线
在抛物线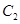 上,试求出
上,试求出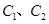 的标准方程;
的标准方程;
(2)求抛物线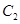 的焦点
的焦点 的坐标并求出椭圆
的坐标并求出椭圆 的离心率;
的离心率;
(3)过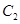 的焦点
的焦点 直线与椭圆
直线与椭圆 交不同两点
交不同两点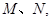 且满足
且满足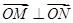 ,试求出直线的方程.
,试求出直线的方程.