如图,设抛物线 (
( )的准线与
)的准线与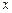 轴交于
轴交于 ,焦点为
,焦点为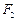 ,以
,以 、
、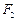 为焦点,离心率
为焦点,离心率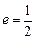 的椭圆
的椭圆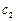 与抛物线
与抛物线 在
在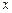 轴上方的一个交点为
轴上方的一个交点为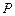 .
.
(1)当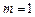 时,求椭圆的方程;
时,求椭圆的方程;
(2)在(1)的条件下,直线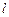 经过椭圆
经过椭圆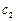 的右焦点
的右焦点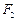 ,与抛物线
,与抛物线 交于
交于 、
、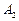 ,如果以线段
,如果以线段 为直径作圆,试判断点
为直径作圆,试判断点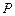 与圆的位置关系,并说明理由;
与圆的位置关系,并说明理由; (3)是否存在实数
(3)是否存在实数 ,使得
,使得 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数 ;若不存在,请说明理由.
;若不存在,请说明理由.
设命题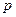 :直线
:直线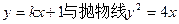 有两个公共点,命题
有两个公共点,命题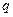 :方程
:方程 表示双曲线,若
表示双曲线,若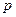 且
且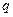 为真,求实数
为真,求实数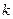 的取值范围.
的取值范围.
已知 是圆
是圆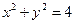 上满足条件
上满足条件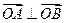 的两个点,其中
的两个点,其中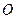 是坐标原点,分别过
是坐标原点,分别过 作
作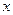 轴的垂线段,交椭圆
轴的垂线段,交椭圆 于
于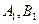 点,动点
点,动点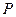 满足
满足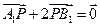
(I)求动点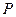 的轨迹方程.
的轨迹方程.
(II)设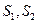 分别表示
分别表示 和
和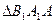 的面积,当点
的面积,当点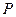 在
在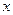 轴的上方,点
轴的上方,点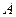 在
在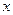 轴的下方时,求
轴的下方时,求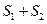 的最大面积.
的最大面积.
如图,正方形 所在平面与圆
所在平面与圆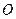 所在平面相交于
所在平面相交于 ,线段
,线段 为圆
为圆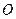 的弦,
的弦,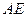 垂直于圆
垂直于圆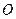 所在平面,垂足
所在平面,垂足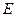 是圆
是圆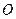 上异于
上异于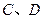 的点,
的点, ,圆
,圆 的直径为
的直径为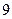 ,
,
1)求证:平面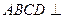 平面
平面 2)求二面角
2)求二面角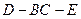 的平面角的正切值.
的平面角的正切值.
若抛物线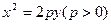 的焦点与椭圆
的焦点与椭圆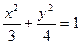 的上焦点重合,
的上焦点重合,
1)求抛物线方程.
2)若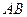 是过抛物线焦点的动弦,直线
是过抛物线焦点的动弦,直线 是抛物线两条分别切于
是抛物线两条分别切于 的切线,求
的切线,求 的交点的纵坐标.
的交点的纵坐标.
如图,四棱锥 中,底面
中,底面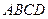 是矩形,
是矩形,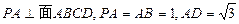 ,点
,点 是
是 的中点,点
的中点,点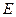 在边
在边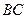 上移动。
上移动。
1)点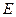 为
为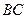 的中点时,试判断
的中点时,试判断 与平面
与平面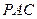 的位置关系,并说明理由。
的位置关系,并说明理由。
2)证明:无论点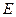 在边
在边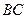 的何处,都有
的何处,都有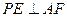
3)当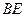 等于何值时,
等于何值时,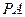 与平面
与平面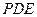 所成角的大小为
所成角的大小为 .
.