四张卡片上分别标有数字“2”、“0”、“0”、“9”，其中“9”可当“6”用，则由这四张卡片可组成不同的四位数的个数为
| A．8 | B．12 | C．24 | D．48 |
已知Sn是等差数列{an}的前n项和,若a1=-10,a4+a6=-4,则当Sn取最小值时,n=( )
| A．5 | B．6 | C．11 | D．5或6 |
已知数列{an}为等差数列,Sn为其前n项和,且a2=3a4-6,则S9等于( )
| A．25 | B．27 | C．50 | D．54 |
已知数列{an}为等差数列,且a3+a7+a11=4π,则tan(a1+a13)=( )
A．- |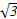
B．± |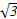
C．± |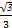
D． |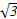
在等差数列{an}中,已知a4+a8=16,则a2+a10=( )
| A．12 | B．16 | C．20 | D．24 |
定义:F(x,y)=yx(x>0,y>0),已知数列{an}满足:an=
(n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为( )
A． |
B．2 | C．3 | D．4 |