若二面角a -l-b 的一个半平面a 上有一个点A，点A到棱l的距离是它到另一个平面b 的距离的2倍，则这个二面角的大小为（ ）．
| A．90° | B．60° | C．45° | D．30° |
已知x，y的取值如表：
| x |
1 |
2 |
3 |
4 |
| y |
2.2 |
3.8 |
5.5 |
6.5 |
从散点图分析，y与x线性相关，且回归方程为
，则a=（）
A.﹣0.15 B.﹣0.26 C.﹣0.35 D.﹣0.61
在回归分析中，残差图中纵坐标为（）
| A．残差 | B．样本编号 | C． |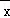
D． |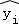
某产品的广告费用x与销售额y的统计数据如下表：
| 广告费用x（万元） |
2 |
3 |
4 |
5 |
| 销售额y（万元） |
27 |
39 |
48 |
54 |
根据上表可得回归方程y=bx+a中的b为9.4，据此模型预报广告费用为6万元时销售额为（）
A.65.5万元 B.66.2万元 C.67.7万元 D.72.0万元
某车间加工零件的数量x与加工时间y的统计数据如表：
| 零件数x（个） |
10 |
20 |
30 |
| 加工时间y（分钟） |
21 |
30 |
39 |
现已求得上表数据的回归方程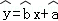
中的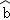
值为0.9，则据此回归模型可以预测，加工100个零件所需要的加工时间约为（）
A.84分钟 B.94分钟 C.102分钟 D.112分钟
某学生四次模拟考试时，其英语作文的减分情况如下表：
| 考试次数x |
1 |
2 |
3 |
4 |
| 所减分数y |
4.5 |
4 |
3 |
2.5 |
显然所减分数y与模拟考试次数x之间有较好的线性相关关系，则其线性回归方程为（）
A.y=0.7x+5.25 B.y=﹣0.6x+5.25 C.y=﹣0.7x+6.25 D.y=﹣0.7x+5.25