一棵树上有一个质量为0.3kg的熟透了的苹果P，该苹果从树上A先落到地面C最后滚入沟底D。已知AC、CD的高度差分别为2.2m和3m，以地面C为零势能面，A、B、C、D、E面之间竖直距离如图所示。已知重力加速度为
，则该苹果从A落下到D的过程中重力势能的减少量和在D处的重力势能分别是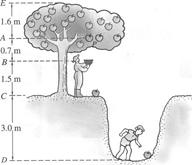
A．15.6J和9J B．9J和－9J
C．15.6J和－9J D．15.6J和－15.6J
如图所示，平行金属导轨与水平面成θ角，导轨与固定电阻R1和R2相连，匀强磁场垂直穿过导轨平面．有一导体棒ab，质量为m，导体棒的电阻与固定电阻R1和R2的阻值均相等，与导轨之间的动摩擦因数为μ，导体棒ab沿导轨向上滑动，当上滑的速度为v时，受到安培力的大小为F.此时( )
| A．电阻R1消耗的热功率为Fv/3 |
| B．电阻R2消耗的热功率为Fv/6 |
| C．整个装置因摩擦而消耗的热功率为μmgvcos θ |
| D．整个装置消耗的机械功率为(F＋μmgcos θ)v |
如图所示，在空间中存在两个相邻的、磁感应强度大小相等、方向相反的有界匀强磁场，其宽度均为L.现将宽度也为L的矩形闭合线圈，从图示位置垂直于磁场方向匀速拉过磁场区域，则在该过程中，能正确反映线圈中所产生的感应电流或其所受的安培力随时间变化的图象是( )
用均匀导线做成的正方形线框边长为0.2 m，正方形的一半放在垂直纸面向里的匀强磁场中，如图甲所示．当磁场以10 T/s的变化率增强时，线框中点a、b两点间的电势差是( )
| A．Uab＝0.1 V | B．Uab＝－0.1 V |
| C．Uab＝0.2 V | D．Uab＝－0.2 V |
如图所示，空间存在两个磁场，磁感应强度大小均为B，方向相反且垂直纸面，MN、PQ为其边界，OO′为其对称轴．一导线折成边长为l的正方形闭合回路abcd，回路在纸面内以恒定速度v0向右运动，当运动到关于OO′对称的位置时( )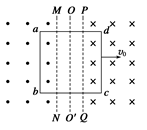
| A．穿过回路的磁通量为零 |
| B．回路中感应电动势大小为2Blv0 |
| C．回路中感应电流的方向为顺时针方向 |
| D．回路中ab边与cd边所受安培力方向相同 |
如图所示，一正方形线圈abcd在匀强磁场中绕垂直于磁感线的对称轴OO′匀速运动，沿着OO′观察，线圈沿逆时针方向转动．已知匀强磁场的磁感应强度为B，线圈匝数为n，边长为l，电阻为R，转动的角速度为ω.则当线圈转至图示位置时( )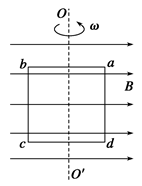
| A．线圈中感应电流的方向为abcda |
B．线圈中的感应电流为 |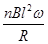
| C．穿过线圈的磁通量为0 |
| D．穿过线圈的磁通量的变化率为0 |