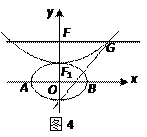
(本小题满分15分)
设 ,椭圆方程为
,椭圆方程为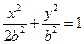 ,抛物线方程为
,抛物线方程为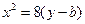 .如图4所示,过点
.如图4所示,过点 作
作 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为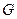 ,已知抛物线在点
,已知抛物线在点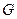 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点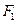 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设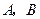 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点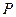 ,使得
,使得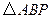 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
一个袋中装有大小相同的黑球、白球和红球.已知袋中共有10个球.从袋中任意摸出1个球,得到黑球的概率是;从袋中任意摸出2个球,至少得到1个白球的概率是.求:
(1)从中任意摸出2个球,得到的都是黑球的概率;
(2)袋中白球的个数.
假设人的某一特征(如眼睛大小)是由他的一对基因所决定的,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人是纯隐性,具有rd基因的人为混合性.纯显性与混合性的人都表露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性.求:
(1)一个孩子有显性基因决定的特征的概率是多少?
(2)两个孩子中至少有一个有显性基因决定的特征的概率是多少?
某射手在一次射击训练中,射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28,计算该射手在一次射击中:
(1)射中10环或9环的概率;
(2)少于7环的概率.
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束.假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立.已知前2局中,甲、乙各胜1局.
(1)求甲获得这次比赛胜利的概率;
(2)求经过5局比赛,比赛结束的概率
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是,每次测试时间间隔恰当,每次测试通过与否互相独立.
(1)求该学生考上大学的概率;
(2)求该学生经过4次测试考上大学的概率.