如图所示，摩托车运动员从高度h=5m的高台上水平飞出，跨越L=10m的壕沟。摩托车以初速度v0从坡底冲上高台的过程历时t=5s，发动机的功率恒为P=1.8kW。已知人和车的总质量为m=180kg（可视为质点），忽略一切阻力。取g=10m/s2。
（1）要使摩托车运动员从高台水平飞出刚好越过壕沟，求他离开高台时的速度大小。
（2）欲使摩托车运动员能够飞越壕沟，其初速度v0至少应为多大？
（3）为了保证摩托车运动员的安全，规定飞越壕沟后摩托车着地时的速度不得超过26m/s，那么，摩托车飞离高台时的最大速度vm应为多少？
测定患者的血沉，在医学上有助于医生对病情作出判断.设血液是由红血球和血浆组成的悬浮液，将此悬浮液放进竖直放置的血沉管内，红血球就会在血浆中匀速下沉，其下沉速率称为血沉.某人的血沉v的值大约是10 mm/h.如果把红血球近似看做是半径为R的小球，且认为它在血浆中下沉时所受的粘滞阻力为Ff=6πηRv.在室温下η=1.8×103 Pa·s.已知血浆的密度ρ0=1.0×103 kg/m3,红血球的密度ρ=1.3×103 kg/m3.试由以上数据估算出红血球半径的大小（结果取一位有效数字即可）.
如图所示，在倾角θ=30°的粗糙斜面上放一物体，重力为G.现用与斜面底边平行的力F=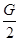
推物体，物体恰能在斜面上做匀速直线运动，求物体与斜面间的动摩擦因数.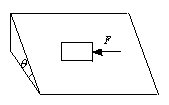
如图所示，将一条轻而柔软的细绳一端固定在天花板上的A点，另一端固定在竖直墙上的B点，A和B到O点的距离相等，绳长为OA的两倍.滑轮的大小与质量均可忽略，滑轮下悬挂一质量为m的重物.设摩擦力可忽略，求平衡时绳所受的拉力为多大？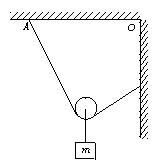
如图所示，用轻绳AC和BC悬挂一重物，绳与水平天花板夹角分别为60°和30°，若物体重100 N，求绳AC和BC所受拉力的大小。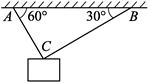
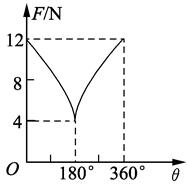
有两个大小不变的共点力，它们的合力大小F随两力夹角变化情况如图所示，则两力大小分别为多少？