(本小题满分14分)已知各项均为正数的数列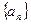 满足
满足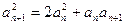 ,且
,且 ,其中
,其中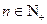 .
.
(Ⅰ)求数列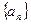 的通项公式;
的通项公式;
(Ⅱ)设数列 的前
的前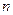 项和为
项和为 ,令
,令 ,其中
,其中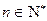 ,试比较
,试比较 与
与 的大小,并加以证明.
的大小,并加以证明.
(本小题满分12分)分别求满足下列条件的直线方程.
(Ⅰ)过点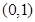 ,且平行于
,且平行于 :
: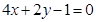 的直线;
的直线;
(Ⅱ)与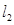 :
: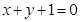 垂直,且与点
垂直,且与点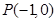 距离为
距离为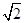 的直线.
的直线.
定义在D上的函数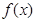 ,如果满足;对任意
,如果满足;对任意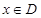 ,存在常数
,存在常数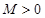 ,都有
,都有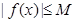 成立,则称
成立,则称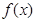 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数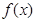 的上界。
的上界。
已知函数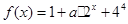 ,
,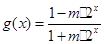
(1)当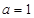 时,求函数
时,求函数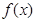 在
在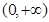 上的值域,并判断函数
上的值域,并判断函数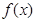 在
在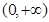 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数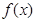 在
在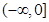 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数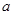 的取值范围;
的取值范围;
(3)若 ,求函数
,求函数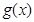 在
在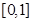 上的上界T的取值范围。
上的上界T的取值范围。
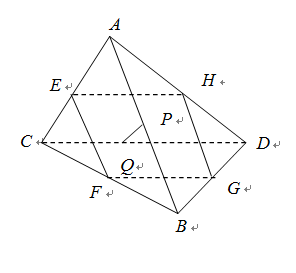
如图,线段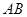 ,
,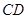 所在直线是异面直线,
所在直线是异面直线,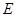 ,
,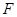 ,
,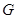 ,
,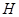 分别是线段
分别是线段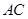 ,
,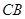 ,
,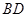 ,
,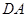 的中点.
的中点.
(1)求证: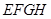
 共面且
共面且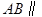 面
面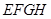 ,
,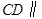 面
面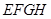 ;
;
(2)设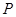 ,
, 分别是
分别是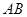 和
和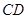 上任意一点,求证:
上任意一点,求证: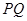 被平面
被平面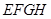 平分.
平分.
|
某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式。
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能是企业获得最大利润,其最大利润约为多少万元。(精确到1万元)。
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;(2)求该几何体的侧面积S。