(本小题满分14分)
已知函数F(x)=|2x-t|-x3+x+1(x∈R,t为常数,t∈R).
(Ⅰ)写出此函数F(x)在R上的单调区间;
(Ⅱ)若方程F(x)-k=0恰有两解,求实数k的值.
(本小题满分12分)
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/米2,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16米,试设计污水池的长和宽,使总造价最低.
(本小题满分12分)
如图,已知三棱锥P=ABC中,PA⊥PC,D为AB的中点,M为PB的中点,且AB=2PD.
(1)求证:DM//面PAC;
(2)找出三棱锥P—ABC中一组面与面垂直的位置关系,并给出证明(只需找到一组即可).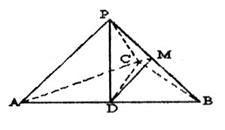
(本小题满分12分)
已知 是公差为正数的等差数列,首项
是公差为正数的等差数列,首项 ,前n项和为Sn,数列
,前n项和为Sn,数列 是等比数列,首项
是等比数列,首项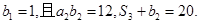
(1)求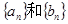 的通项公式.
的通项公式.
(2)令 的前n项和Tn.
的前n项和Tn.
.(本小题满分12分)
已知函数
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)△ABC内角A、B、C的对边长分别为a、b、c,若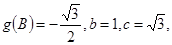
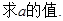
(本小题满分14分)
已知一非零向量列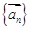 满足:
满足: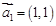 ,
,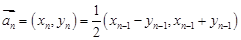
 .
.
(1)证明: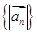 是等比数列;
是等比数列;
(2)设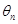 是
是 的夹角
的夹角 ,
,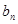 =
=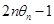 ,
, ,求
,求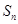 ;
;
(3)设
 ,问数列
,问数列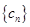 中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.