、(本小题满分12分)某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.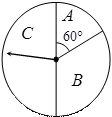
(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为 (元).求随机变量
(元).求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知矩形纸片ABCD中,AB=6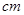 ,AD=12
,AD=12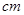 ,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点,M、N分别位于边AB、BC上,设
,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点,M、N分别位于边AB、BC上,设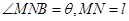 .
.
(ⅰ)试将 表示成
表示成 的函数;
的函数;
(ⅱ)求 的最小值.
的最小值.
已知函数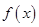 满足
满足 ,其中
,其中 且
且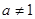 .
.
(1)对于函数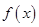 ,当
,当 时,
时, ,求实数
,求实数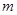 值的集合;
值的集合;
(2)当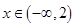 时,
时,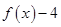 值恒为负数,求
值恒为负数,求 的范围.
的范围.
如图,过点 的两直线与抛物线
的两直线与抛物线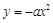 相切于A、B两点, AD、BC垂直于直线
相切于A、B两点, AD、BC垂直于直线 ,垂足分别为D、C.
,垂足分别为D、C.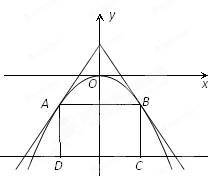
(1)若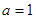 ,求矩形ABCD面积;
,求矩形ABCD面积;
(2)若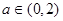 ,求矩形ABCD面积的最大值.
,求矩形ABCD面积的最大值.
已知函数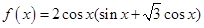
(1)求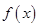 的值域和最小正周期;
的值域和最小正周期;
(2)若对任意 ,使得
,使得 恒成立,求实数
恒成立,求实数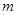 的取值范围.
的取值范围.
已知命题 :函数
:函数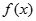 为
为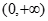 上单调减函数,实数
上单调减函数,实数 满足不等式
满足不等式 .命题
.命题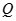 :当
:当 ,函数
,函数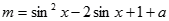 .若命题
.若命题 是命题
是命题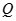 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围。
的取值范围。