已知万有引力常量G，地球半径R，月球和地球球心之间的距离r，同步卫星距地面的高度h，月球绕地球的运转周期T1，地球的自转周期T2，地球表面的重力加速度为g．某同学根据以上条件，提出一种估算地球质量M的方法：
同步卫星绕地球作圆周运动，由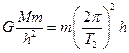
得：
⑴请判断上面的结果是否正确，并说明理由；如不正确，请给出正确的解法和结果；
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果．
如图所示，木块质量m＝0.78 kg，在与水平方向成q＝37°角、斜向右上方和恒定拉力F作用下，以a＝2.0 m/s2的加速度从静止开始做匀加速直线运动，在3 s末时撤去拉力F。已知木块与地面间的动摩擦因数m＝0.4，取重力加速度g＝10 m/s2，sin37°＝0.6，cos37°＝0.8。求：（1）拉力F的大小（2）物体在5 s内滑行的总位移。
如图所示，质量m＝1kg的小球套在细斜杆上，斜杆与水平方向成a＝30°角，球与杆之间的滑动摩擦因数m＝
，球在竖直向上的拉力F＝20N作用下沿杆向上滑动．g取10m/s2．求（1）在图中画出小球的受力图．（2）求球对杆的压力大小和方向．（3）小球的加速度多大？
如图所示，轨道ABO在同一竖直平面内，由光滑水平轨道OB和倾角θ=30°、高度h=1m的倾斜轨道BA连接而成， OB与BA连接处是半径很小的圆弧，水平轨道上一轻质弹簧左端O固定在竖直的墙上，质量m=0.5kg的小物块从BA轨道上A点由静止开始下滑。已知物块与倾斜轨道间的动摩擦因数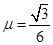
，重力加速度g=10m/s2，弹簧形变始终在弹性限度内．求：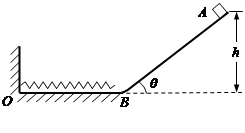
（1）物块第一次在水平轨道上压缩弹簧运动到速度为零时，弹簧具有的弹性势能EP；
（2）物块在倾斜轨道上滑动的总路程s；
（3）物块第n次压缩弹簧后，沿倾斜轨道上升的最大高度hn．
某人站在一平台上，用长L=0.6m的轻细线拴一个质量为m=0.6kg的小球，让它在竖直平面内以O点为圆心做圆周运动，当小球转到最高点A时，人突然撒手．经0.8s小球落地，落地点B与A点的水平距离BC=4.8m，不计空气阻力，g=10m/s2．求：
（1） A点距地面高度；
（2） 小球离开最高点时的线速度及角速度大小；
（3）人撒手前小球运动到A点时，绳对球的拉力大小．
静止在水平面上的物体的质量为2 kg，在水平恒力F推动下从静止开始做匀加速直线运动，4 s末它的速度达到4 m/s，此时将F撤去，物体做匀减速直线运动，又经6 s物体停下来，如果物体与地面的动摩擦因数不变，求：
（1）前4s内的加速度；
（2）前4s内的位移；
（3）F的大小．