如图甲所示,M、N为水平放置的平行板电容器的两个极板,极板长L="0.2" m,两板间距d=0.1m,在M、N间加上如图乙所示的电压,一个带电粒子的电量q =+1.0×10-6C、质量m=1.0×10-8kg,粒子重力不计,求:
(1)0~1×10-3s电容器内部场强的大小和方向;
(2)若在t=0的时刻,将上述带电粒子从紧靠M板中心处无初速释放,求粒子从M板运动到N板所经历的时间t;
(3)若在t=0的时刻,上述带电粒子从靠近M板的左边缘处以初速度v0水平射入两极板间,且粒子沿水平方向离开电场,求初速度v0的大小。
在“互成角度的两个共点力的合成”实验中,如图所示,用AB两弹簧秤拉橡皮条结点O,使其位于E处,此时(α+ β)= 900,然后保持A的读数不变,当α角由图中所示的值逐渐减小时,要使结点仍在E处,可采取的办法是()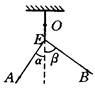
| A.增大B的读数,减小β角 |
| B.减小B的读数,减小β角 |
| C.减小B的读数,增大β角 |
| D.增大B的读数,增大β角 |
为了探求弹簧弹力F和弹簧伸长量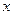 的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为.这两根弹簧的劲度系数分别为:甲弹簧为N/m,乙弹簧为N/m.若要制作一个精确度较高的弹簧秤,应选弹簧(填“甲”或“乙”).
的关系,李强同学选了甲、乙两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线是因为.这两根弹簧的劲度系数分别为:甲弹簧为N/m,乙弹簧为N/m.若要制作一个精确度较高的弹簧秤,应选弹簧(填“甲”或“乙”).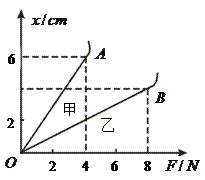
在“互成角度的两个共点力的合成”实验中,其中的三个步骤:
①在水平放置的木板上垫一张白纸,把橡皮条的一端固定在木板上,另一端拴两根细线,通过细线同时用两个测力计互成角度地拉橡皮条,使它与细线的结点到达某一位置O点,在白纸上记下O点和两测力计的读数F1和F2.
②在纸上根据F1和F2的大小,应用平行四边形定则作图求合力F.
③只用一只测力计通过细绳拉橡皮条,使它的伸长量与两测力计拉时相同,记下此时测力计的读数F′和细绳的方向.
以上三个步骤均有错误或疏漏,请指出:
①中是______________________________________________________________;
②中是______________________________________________________________;
③中是______________________________________________
在“合力与分力之间的关系”实验中,橡皮条一端固定在木板上,用两个弹簧秤把橡皮条的另一端拉到某一位置O点,以下操作正确的是()
| A.实验中必须记录弹簧秤拉力的方向 |
| B.在实验中,弹簧秤必须保持与木板平行,读数时视线要正对弹簧秤的刻度 |
| C.实验中,先将其中一个弹簧秤沿某一方向拉到最大量程,然后只需调节另一弹簧秤的拉力大小和方向,把橡皮条节点拉到O点 |
| D.实验中,把橡皮条节点拉到O点时,两弹簧秤之间的夹角应取90°不变,以便于计算合力的大小 |
在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的一另一端都有绳套(如图).实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉像皮条.某同学认为在此过程中必须注意以下几项:
A.两根细绳必须等长
B.橡皮条应与两绳夹角的平分线在同一直线上.
C.在使用弹簧秤时要注意使弹簧秤与木板平面平行.
其中正确的是 .(填入相应的字母)