(本小题满分14分)
已知正数数列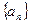 满足:
满足: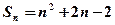 ,其中
,其中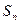 为数列
为数列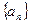 的前
的前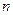 项和.
项和.
(1)求数列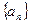 的通项
的通项 ;
;
(2)令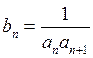 ,求
,求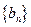 的前n项和Tn.
的前n项和Tn.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且 底面ABCD,
底面ABCD, ,E是PA的中点.
,E是PA的中点.
(1)求证:平面 平面EBD;
平面EBD;
(2)若PA=AB=2,求三棱锥P-EBD的高.
某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
在公差不为0的等差数列 中,
中, ,且
,且 成等比数列.
成等比数列.
(1)求 的通项公式;
的通项公式;
(2)设 ,试比较
,试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
已知函数 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若 时,
时, ,求a的取值范围.
,求a的取值范围.
长为3的线段两端点A,B分别在x轴正半轴和y轴的正半轴上滑动, ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
(1)以直线AB的倾斜角 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程;
(2)求点P到点 距离的最大值.
距离的最大值.