利用数学归纳法证明“1+a+a2+…+an+1=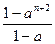 , (a≠1,n∈N)”时,在验证n=1成立时,左边应该是 ( )
, (a≠1,n∈N)”时,在验证n=1成立时,左边应该是 ( )
| A.1 | B.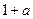 |
C. |
D.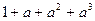 |
下列说法正确的是()
A.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.若命题 ,则命题 ,则命题 |
C.命题“若 ,则 ,则 ”的逆否命题为真命题 ”的逆否命题为真命题 |
D.“ ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
设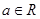 则
则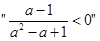 是“
是“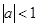 ”成立的 ( )
”成立的 ( )
| A.充分必要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既非充分也非必要条件 |
对任意的实数 ,若
,若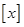 表示不超过
表示不超过 的最大整数,则
的最大整数,则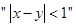 是
是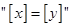 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题p: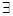
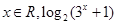 ≤0,则( )
≤0,则( )
A.p是假命题; p: p: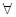 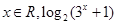 ≤0 ≤0 |
B.p是假命题; p: p: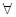 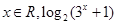 >0 >0 |
C.p是真命题; p: p: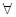 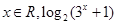 ≤0 ≤0 |
D.p是真命题; p: p: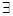 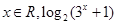 >0 >0 |
“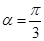 ”是“
”是“ ”的
”的
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |