如图 (a)所示,质量m=2.0kg的物体静止在水平面上,物体与水平面间的动摩擦因数μ=0.2.从t=0时刻起,物体受到一个水平力F的作用而开始运动,前8s内F随时间t变化的规律如图 (b)所示.g取10m/s2求:
(l)在图 (c)的坐标系中画出物体在前8s内的v-t图象.(要求有计算过程)
(2)前8s内物体的位移
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量均为Q,其中A带正电荷,B带负电荷,D、C是它们连线的垂直平分线,A、B、C三点构成一边长为d的等边三角形,另有一个带电小球E,质量为m、电量为+q(可视为点电荷),被长为L的绝缘轻质细线悬挂于O点,O点在C点的正上方。现在把小球E拉到M点,使细线水平绷直且与A、B、C处于同一竖直面内,并由静止开始释放,小球E向下运动到最低点C时,速度为v。已知静电力常量为k,若取D点的电势为零,试求: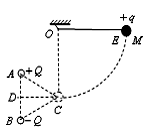
(1)在A、B所形成的电场中,M点的电势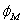 。
。
(2)绝缘细线在C点所受到的拉力T。
一个初速度为零的电子在U1=45V的电压作用下得到一定速度后垂直于平行板间的匀强电场飞入两板间的中央,如图所示。若平行板间的距离d=1cm,板长l=1.5cm,电子的电荷量e="1.6×10" -19C,电子的质量m="9×10" -31kg,求: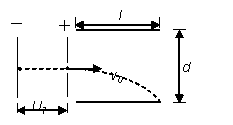
(1)电子进入平行板间的速度v0多大?
(2)若电子恰能沿平行板右边缘射出,加在平行板上的电压U2为多大?
如图所示电路中,电阻R1=R2=3Ω,R3=6Ω,S扳至1时,电流表的示数为1.0A, S扳至2时,电流表示数为1.5A,求: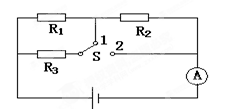
(1)电源的电动势E和内阻r(电流表内阻不计);
(2)S扳至2时,电源的输出功率。
一根长为L的丝线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成37o角,(重力加速度为g),求:
(1)该静止小球带何种电;
(2)匀强电场的电场强度的大小;
物体从高H处自由落下,最后1秒内运动位移是 H.求
H.求
⑴物体下落的时间.⑵物体下落的高度H。(g="10" m/s2))