在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形
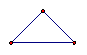
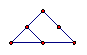
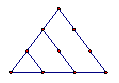
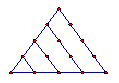
1 3 6 10 15
则第 个三角形数为
个三角形数为
A. |
B. |
C. |
D.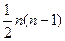 |
已知命题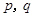 ,若命题“
,若命题“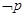 ”与命题“
”与命题“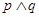 ”都是假命题,则()
”都是假命题,则()
A.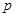 为真命题, 为真命题,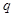 为假命题 为假命题 |
B.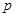 为假命题, 为假命题,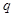 为真命题 为真命题 |
C.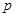 , ,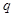 均为真命题 均为真命题 |
D.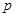 , ,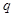 均为假命题 均为假命题 |
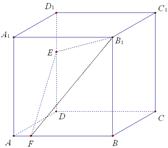
如图,正方体 中,
中,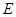 ,
,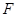 分别为棱
分别为棱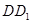 ,
,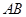 上的点. 已知下列判断:①
上的点. 已知下列判断:①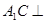 平面
平面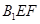 ;②
;②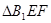 在侧面
在侧面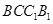 上的正投影是面积为定值的三角形;③在平面
上的正投影是面积为定值的三角形;③在平面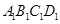 内总存在与平面
内总存在与平面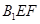 平行的直线;④平面
平行的直线;④平面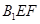 与平面
与平面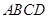 所成的二面角(锐角)的大小与点
所成的二面角(锐角)的大小与点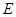 的位置有关,与点
的位置有关,与点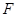 的位置无关. 其中正确判断的个数有()
的位置无关. 其中正确判断的个数有()
| A.1个 | B.2个 | C.3个 | D.4个 |
已知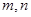 是两条不同直线,
是两条不同直线, 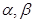 是两个不同平面.下列命题中不正确的是()
是两个不同平面.下列命题中不正确的是()
A.若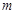 ∥ ∥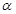 , ,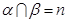 ,则 ,则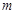 // //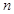 |
B.若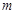 // //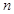 , ,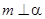 ,则 ,则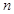 ⊥ ⊥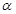 |
C.若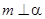 , ,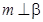 ,则 ,则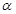 ∥ ∥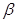 |
D.若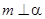 , ,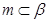 ,则 ,则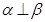 |
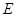 ,
,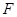 是等腰直角△
是等腰直角△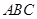 斜边
斜边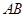 上的三等分点,则
上的三等分点,则 ()
()
A.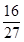 |
B.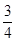 |
C.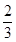 |
D.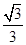 |
从 中随机抽取一个数记为
中随机抽取一个数记为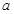 ,从
,从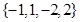 中随机抽取一个数记为
中随机抽取一个数记为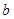 ,则函数
,则函数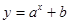 的图象经过第三象限的概率是()
的图象经过第三象限的概率是()
A.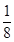 |
B.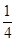 |
C.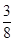 |
D.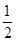 |