如图所示,固定在竖直面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接,轨道半径R=0.5m,一质量m=0.2kg的小物块(可视为质点)放在水平轨道上的A点,A与B相距L=10m,物块与水平轨道间的动摩擦因数μ=0.1。现用一水平恒力F向右推物块,已知F=3N,当物块运动到C点时撤去该力,设C点到A点的距离为x。在圆轨道的最高点D处安装一压力传感器,当物块运动到D点时传感器就会显示相应的读数FN,压力传感器所能承受的最大压力为90N,g取10m/s2。
(1)要使物块能够安全通过圆轨道的最高点D,求x的范围;
(2)在满足(1)问的情况下,在坐标系中作出压力传感器的读数FN与x的关系图象。
边长为L的正方形单匝线圈abcd,每条边的电阻均为R,以cd边为轴以角速度ω在磁感应强度为B的磁场中从图示位置匀速转动,cd两端接有一个阻值也为R的电阻。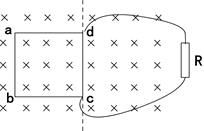
求:
(1)线圈产生的感应电动势的表达式
(2)经过t秒,电阻上产生的焦耳热是多少?
国际空间站是迄今最大的太空合作计划,其离地高度为H,绕地球运动的周期为T1。通过查找资料又知万有引力常量G,地球半径R,同步卫星距地面的高度h,地球的自转周期T2以及地球表面重力加速度g。
某同学根据以上条件,提出一种估算地球质量M的方法:
同步卫星绕地心做圆周运动,由  得
得 
(1)请判断上面得出的结果是否正确,请说明理由;如不正确,请给出正确解法和结果。
(2)请根据题给条件再提出两种估算地球质量的方法,并解得结果。
如图所示,光滑半圆管R=0.4m,竖直放置,两个质量均为m=2kg的小球A、B以不同的速度进入管内.A通过最高点C时,对管壁上部压力为60N,B通过最高点C时,对管壁下部压力为15N。(g=10m/s2),求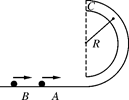
(1)A 球、B球在最高点的速率。
(2)A、B两球落地点间的距离.
质量为m的球用长为L的细绳悬于天花板的O点,并使之在水平面内做匀速圆周运动,细线与竖直线成θ角,求
(1)画出小球的受力示意图
(2)小球做匀速圆周运动线速度的大小
在勇气号火星探测器着陆的最后阶段,着陆器降落到火星表面上,再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后,到达最高点时高度为h,速度方向是水平的,速度大小为υ0,求它第二次落到火星表面时速度的大小,计算时不计大气阻力。已知火星的一个卫星的圆轨道的半径为r,周期为T,火星可视为半径为r0的均匀球体。