如图甲所示是游乐场中过山车的实物图片，图乙是由它抽象出来的理想化模型（圆形轨道与斜轨道之间平滑连接，不计摩擦和空气阻力）。已知圆轨道的半径为R，质量为m的小车（视作质点）从P点由静止沿斜轨道下滑，进入圆轨道后沿圆轨道运动。已知P点到圆轨道最低点B的高度差H＝3R，通过计算说明小车能否顺利通过最高点A。若能顺利通过，小车在A点受到的压力有多大？
如图所示，极板A、B、K、P连入电路，极板P、K，A、B之间分别形成电场，已知电源电动势E=300V，电源内阻不计 ，电阻R1="2000KΩ," R2=1000KΩ，A、B两极板长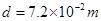
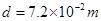，间距。一个静止的带电粒子，电荷量
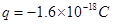、质量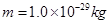
，从极板K中心经 P、K间电场加速后，进入极板A、B间电场中发生偏转。（极板间电场可视为匀强电场且不考虑极板边缘效应，不计粒子重力）求：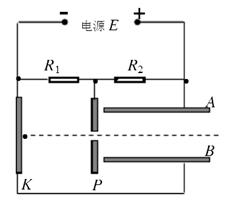
⑴极板P、K之间电压UPK，A、B之间电压UAB
⑵粒子刚进入偏转极板A、B时速度v0
⑶粒子通过极板A、B时发生偏转距离y
如图所示，电阻R1＝2 Ω，小灯泡L上标有“3 V、1.5 W”字样，电源的内阻为r＝1 Ω，滑动变阻器的最大阻值为R0(大小未知)．当触头P滑动到最上端a时，电流表的读数为1 A，小灯泡L恰好正常发光，求：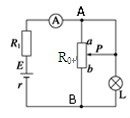
(1)滑动变阻器的最大阻值R0；
(2)当触头P滑动到最下端b时，电源的总功率及输出功率．
(3)不需要说明理由，判断当电路A、B两点间元件消耗的电功率
最大时，触头P的位置（假定小灯泡电阻保持不变）．
如图，真空中有两个点电荷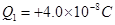
和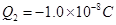
，分别固定在x=0和x="6" cm的位置上。静电力常量k=9.0×109N·m2/C2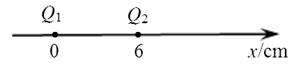
(1)x坐标轴上电场强度为0的位置坐标是什么?
(2)坐标轴上x=3cm处场强的大小和方向？
如图所示，质量m＝1kg的物体在F=20N水平向右的拉力作用下由静止开始沿足够长的斜面向上滑动，斜面固定不动且与水平方向成a＝37°角，物体与斜面之间的动摩擦因数μ=0.25，拉力F作用物体2s后撤去。（g=10m/s2，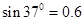
，
）
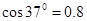试求：（1）物体在力F的作用下运动时对斜面的压力大小；
（2）物体在力F的作用下运动时加速度的大小；
（3）撤去力F作用后物体沿斜面向上运动的最大距离。
一个物体做匀变速直线运动，初速度10m/s,方向向东，5s后物体的速度为15m/s,方向向西，试求：
（1）物体运动的加速度的大小；
（2）这5s内物体运动的位移的大小及方向；
（3）这5s内物体运动的路程。