用反证法证明命题“
”,其反设正确的是
A． |
B． |
C． |
D． |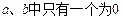
已知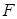
是抛物线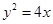
的焦点,准线与
轴的交点为
，点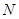
在抛物线上,且
,则
等于（）
A． |
B． |
C． |
D． |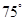
已知函数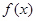
的导函数为
，且满足
，则
（）
A． |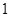
B． |
C． |
D．无法确定 |
命题
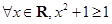，则
是( )
A． |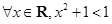
B． |
C． |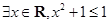
D． |
把函数
的图像向左平移
个单位，所得图像的解析式是（）
A． |
B． |
C． |
D． |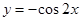
有如下几个结论：
①相关指数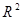
越大，说明残差平方和越小，模型的拟合效果越好；
②回归直线方程：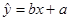
一定过样本点的中心：（
；
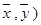③残差点比较均匀地落在水平的带状区域中，说明选用的模型比较合适；
④在独立性检验中，若公式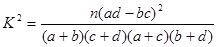
中的
的值越大，说明“两个分类变量有关系”的可能性越强.
其中正确结论的个数有（）个.
| A．1 | B．3 | C．2 | D．4 |