大小相同质量不等的A、B两球,在光滑水平面上作直线运动,发生正碰撞后分开.已知碰撞前A的动量pA=20㎏·m/s,B的动量pB=-30㎏·m/s,碰撞后A的动量pA=-4㎏·m/s,则:
(1)碰撞后B的动量pB;
(2)碰撞过程中A受到的冲量;
(3)若碰撞时间为0.01s,则B受到的平均冲力大小.
如图甲所示,A、B两块金属板水平放置,相距为d="0." 6 cm,两板间加有一周期性变化的电压,当B板接地(φB=0)时,A板电势φA,随时间变化的情况如图乙所示.现有一带负电的微粒在t=0时刻从B板中央小孔射入电场,若该带电微粒受到的电场力为重力的两倍,且射入电场时初速度可忽略不计.求:(g="10" m/s2).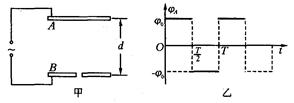
(1)在0~ 和
和 ~T这两段时间内微粒的加速度大小和方向;
~T这两段时间内微粒的加速度大小和方向;
(2)若该微粒上升到最高点时速度恰好达到最大,所加电压的周期T为多少
(3)若该微粒上升到最高点时恰好不与A板相碰,所加电压的周期T为多少
如图所示,M为一线圈电阻rM=0.4Ω的电动机,R=24Ω,电源电动势E=40V.当S断开时,电流表的示数,I1=1.6A,当开关S闭合时,电流表的示数为I2=4.0A求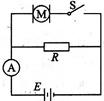
(1)电源内阻
(2)开关S闭合时电动机输出的机械功率
(3)开关S闭合时电源输出功率
如图,一带电液滴在重力和场力的作用下,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°。已知带电液滴的质量为m,水平方向的电场强度为E,带电液滴从b运动到d所用时间为t,重力加速度为g。求: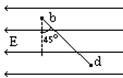
(1)带电液滴带何种电?带电量为多少?
(2)从b运动到d,带电液滴的电势能变化多少?是增加还是减少?
一束电子流(电子质量为m,电量绝对值为e)经电压为U的加速电场加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图所示,若两板间距为d,板长为l,那么,要使电子能从平行板间飞出,则
(1)电子进入偏转电场的速度大小是多少?
(2)两个极板上最多能加多大的偏转电压U′?
在B=2T的匀强磁场中放一根与磁场方向垂直、长度为0.8m的通电直导线,若导线中的电流为5A,求:(1)导线受到的安培力
(2)若将导线沿磁场方向移动了0.5m,求安培力对导线所做的功。