如图所示,水平面上有两根相距0.5 m的足够长的平行金属导轨MN和PQ,它们的电阻可忽咯不计,在M和P之间接有阻值为R的定值电阻,导体棒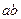 长L=0.5m,其电阻为r,与导轨接触良好。整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4 T。现使
长L=0.5m,其电阻为r,与导轨接触良好。整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4 T。现使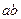 以
以 的速度向右做匀速运动。求:
的速度向右做匀速运动。求:
(1)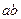 中的感应电动势多大?
中的感应电动势多大?
(2)ab中电流的方向如何?
(3)若定值电阻R=3.0Ω,导体棒的电阻r=1.0Ω,则电路中的电流多大?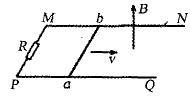
如图所示,一根光滑绝缘细杆与水平面成α=30°的角倾斜固定.细杆的一部分处在场强方向水平向右的匀强电场中,场强E=2×104N/C.在细杆上套有一个带电量为q=-1.73×10-5C、质量为m=3×10-2kg的小球.现使小球从细杆的顶端A由静止开始沿杆滑下,并从B点进入电场,小球在电场中滑至最远处的C点.已知AB间距离s1=0.4 m,g=10 m/s2.求: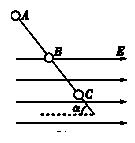
(1)小球在B点的速度vB .
(2)小球进入电场后滑行的最大距离s2 .
(3)小球从A点滑至C点的时间是多少?
如图所示,一根长为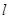 的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=370时,小球处于平衡状态,(sin370=0.6)试求:
的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场,电场强度大小为E,方向水平向右,已知:当细线偏离竖直方向为θ=370时,小球处于平衡状态,(sin370=0.6)试求: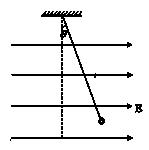
(1)小球带何种电荷,带电量为多少;
(2)如果将细线剪断,小球经时间t发生的位移大小;
(3) 若将小球拉至最低点无初速释放,当小球运动到图示位置时受到线的拉力的大小。
如图所示,一根柔软的弹性绳子右端固定在竖直墙壁上,现在绳上每隔0.20m标记一个点,分别记为A、B、C、D、E…,拉着绳子的左端点A使其上下做简谐运动时,绳上便形成一列向右传播的简谐横波.若A点从平衡位置开始起振,且经0.2s第一次达到最大位移处,此时C点恰好开始振动.求:简谐振动周期和波的传播速度.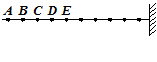
如图所示,固定在水平地面上的圆筒气缸内有一定质量的理想气体,气缸壁是导热的,缸外环境保持恒温,活塞与气缸壁的接触是光滑的,且不漏气.已知外界大气压强为P0,活塞面积为S,活塞厚度不计,开始时活塞处于气缸中央位置,求:将活塞缓慢地向右移动至气缸右端口时的水平拉力F大小.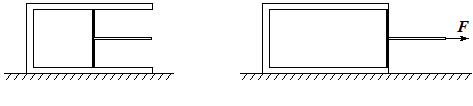
如图所示,半径为R的圆形区域内、外有方向相反的与圆平面垂直的匀强磁场,圆形区域外的匀强磁场范围足够大,磁感应强度大小均为B.一质量为m、电量为q的带正电粒子从圆弧上P点正对圆心O以速度v进入圆形区域内的磁场,经过时间 从Q点进入圆形区域外的磁场,不计粒子重力.求:
从Q点进入圆形区域外的磁场,不计粒子重力.求:
(1)粒子在圆形区域内的磁场中做匀速圆周运动的半径r;
(2)粒子从P点开始经Q点回到P点的最短时间t2;
(3)若粒子从P点以速度 正对圆心O进入圆形区域内的磁场,则粒子是否能在圆形区域内、外磁场中做周期性运动,如果不能,请说明理由;如果能,试求出这个周期.
正对圆心O进入圆形区域内的磁场,则粒子是否能在圆形区域内、外磁场中做周期性运动,如果不能,请说明理由;如果能,试求出这个周期.