为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛,为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计。请你根据表中信息解答下列问题:
(1)若用系统抽样的方法抽取容量为50的一个样本,则写出表中的①②③④⑤填的数据;
(2)作出频率分布直方图;
(3)试估计参加这次竞赛的学生的平均成绩
| 分组 |
频数 |
频率 |
| 60.5~70.5 |
① |
0.16 |
| 70.5~80.5 |
10 |
② |
| 80.5~90.5 |
18 |
0.36 |
90.5~100. 5 5 |
③ |
④ |
| 合计 |
50 |
⑤ |
(本小题满分14分)如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形,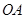 ⊥平面
⊥平面 ,
, 为
为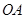 的中点,
的中点, 为
为 的中点,
的中点,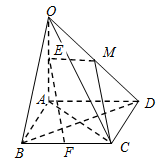
求证:(Ⅰ)平面 ⊥平面
⊥平面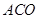 ;(Ⅱ)
;(Ⅱ)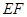 //平面
//平面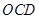 .
.
)已知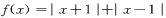 ,不等式
,不等式 的解集为M.
的解集为M.
(I)求M;
(II)当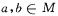 时,证明:
时,证明: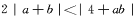 .
.
如图,AB是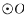 的弦,C、F是
的弦,C、F是 上的点,OC垂直于弦AB,过点F作
上的点,OC垂直于弦AB,过点F作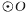 的切线,交AB的延长线于D,连结CF交AB于点E.
的切线,交AB的延长线于D,连结CF交AB于点E.
(I) 求证: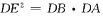 ;
;
(II)若BE = 1,DE = 2AE,求 DF 的长.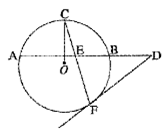
已知函数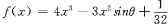 ,其中
,其中 为参数,且
为参数,且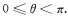
(I)当 时,判断函数
时,判断函数 是否有极值,说明理由;
是否有极值,说明理由;
(II)要使函数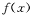 的极小值大于零,求参数
的极小值大于零,求参数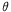 的取值范围;
的取值范围;
(III)若对(II)中所求的取值范围内的任意参数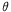 ,函数
,函数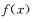 在区间(2a-1,a)内都是增函数,求实数a的取值范围.
在区间(2a-1,a)内都是增函数,求实数a的取值范围.
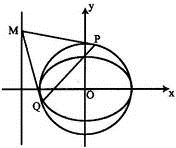
已知椭圆E: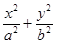 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e=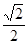 ,且经过点(
,且经过点(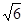 ,1),O为坐标原点。
,1),O为坐标原点。
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)圆O是以椭圆E的长轴为直径的圆,M是直线x=-4在x轴上方的一点,过M作圆O的两条切线,切点分别为P、Q,当∠PMQ=60°时,求直线PQ的方程.