如图所示,一光滑的半圆形轨道处于竖直平面内,并和一粗糙的斜面相接,其半径大小为R=0.4m,直径BC在竖直方向上,一小物体放在斜面上的A点,离水平面高度为h=3m,小物体与斜面之间的动摩擦因数为μ=0.5,斜面倾角θ=37o。已知sin37o=0.6,cos37o=0.8,重力加速度g=10m/s2,现在把小物体从静止开始自由释放,求: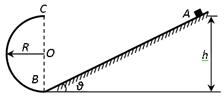
(1)小物体运动到斜面底端B点时速度的大小?
(2)证明小物体可以沿半圆形轨道运动到最高点C;
(3)小物体离开半圆轨道后第一次落到斜面上时,其速度v的大小
质量为m=0.8 kg的砝码悬挂在轻绳PA和PB的结点上并处于静止状态。.PA与竖直方向的夹角37°,PB沿水平方向。质量为M=10kg的木块与PB相连,静止于倾角为37°的斜面上,如图所示。g取10N/kg,sin37°=0.6,cos37°=0.8.求: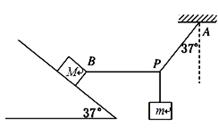
(1)轻绳PB拉力的大小;
(2)木块所受斜面的摩擦力和弹力大小.
如图所示,物体B放在粗糙的水平桌面上,A被三根细绳悬挂,物体A、B都处于静止状态,其质量分别为mA=2kg,mB=5kg,细绳OB呈水平,细绳OP与竖直方向成37 º角。(已知sin37 º=0.6; cos37 º=0.8)求: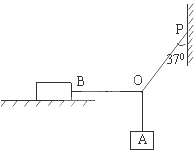
(1)请在图上画出结点O的受力示意图
(2)物体B受到的摩擦力
(3)若将B物体固定在桌面上,OA、OB、OP细绳的位置保持不变,且三细绳所能承受的最大张力都是50N,为了使细绳不断,则所挂的A物的最大重量是多少?
汽车先以a1=0.5m/s2的加速度由静止开始做匀加速直线运动,在20s末改做匀速直线运动,当匀速运动持续10s后,因遇到障碍汽车便紧急刹车,不考虑人的反应时间。已知汽车刹车的加速度为a2=-2m/s2,求:
(1)汽车匀速运动时的速度大小
(2)汽车刹车后6s内所通过的位移大小
(3)在坐标图上画出该汽车运动全过程的速度一时间图象
一物体以20m/s的初速度向东做匀减速直线运动,ls末速度减为16m/s,求:
(1)物体的加速度
(2)5s末的速度是多少?
(3)物体在5s内的位移大小
如图甲所示,水平光滑的桌面上静止放置一条长为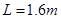 的纸带,纸带上正中间位置放置有一质量为
的纸带,纸带上正中间位置放置有一质量为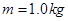 的小铁块,纸带的左边恰好在桌面的左边缘,小铁块与纸带间的动摩擦因数为
的小铁块,纸带的左边恰好在桌面的左边缘,小铁块与纸带间的动摩擦因数为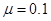 .现让纸带从
.现让纸带从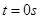 时刻开始一直保持
时刻开始一直保持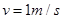 的速度向左匀速运动.已知桌面高度为
的速度向左匀速运动.已知桌面高度为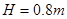 ,
,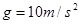 ,小铁块在运动过程中不翻滚,不计空气阻力.求:
,小铁块在运动过程中不翻滚,不计空气阻力.求: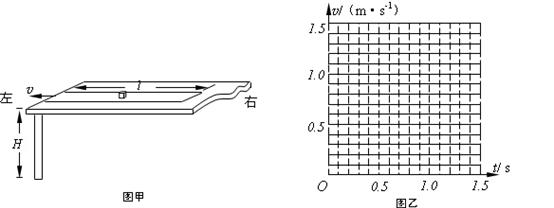
(1)小铁块从开始运动到桌面边缘过程所经历的时间并在乙图画出此过程中小铁块的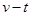 图象;
图象;
(2)小铁块抛出后落地点到抛出点的水平距离;
(3)小铁块从开始运动到桌面边缘过程中产生的内能。