某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如题图所示不用完全相同的轻绳将个大小相同、质量不等的小球并列悬挂于一水平杆、球间有微小间隔,从左到右,球的编号依次为1、2、3……,球的质量依次递减,每球质量与其相邻左球质量之比为.将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞……所有碰撞皆为无机械能损失的正碰.(不计空气阻力,忽略绳的伸长,取10 )
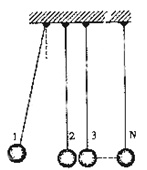
(1)设与号球碰撞前,号球的速度为,求号球碰撞后的速度.
(2)若=5,在1号球向左拉高的情况下,要使5号球碰撞后升高16(16 小于绳长)问值为多少?
(3)在第(2)问的条件下,悬挂哪个球的绳最容易断,为什么?
一静止的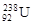 核衰变为
核衰变为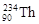 核时,只放出一个α粒子,已知
核时,只放出一个α粒子,已知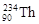 的质量为MT,α粒子质量为Mα,衰变过程中质量亏损为△m,光在真空中的速度为c,若释放的核能全部转化为系统的动能,求放出的α粒子的初动能。
的质量为MT,α粒子质量为Mα,衰变过程中质量亏损为△m,光在真空中的速度为c,若释放的核能全部转化为系统的动能,求放出的α粒子的初动能。
(14分)如图所示,AOB是1/4圆柱玻璃砖的截面图,玻璃的折射率为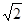 .今有一束平行光线以450的入射角入射到玻璃砖的AO面,这些光线只有一部分能从AB面射出,并假设凡是射到OB面上的光线全部被吸收,也不考虑OA面的反射作用.试求圆柱AB面上能射出光线的面积占AB表面积的几分之几?
.今有一束平行光线以450的入射角入射到玻璃砖的AO面,这些光线只有一部分能从AB面射出,并假设凡是射到OB面上的光线全部被吸收,也不考虑OA面的反射作用.试求圆柱AB面上能射出光线的面积占AB表面积的几分之几?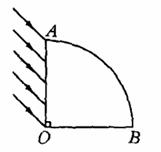
一根质量分布均匀的长直绳AB,在水平恒定外力F的作用下,沿光滑水平面以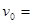 2m/s的初速度做匀加速直线运动(忽略绳子的形变),在头2s内所通过的位移等于绳长的6倍。如图甲所示,绳内距A端x处的张力(即绳内部之间的拉力)
2m/s的初速度做匀加速直线运动(忽略绳子的形变),在头2s内所通过的位移等于绳长的6倍。如图甲所示,绳内距A端x处的张力(即绳内部之间的拉力) 的关系如图乙所示,利用图象和题中的已知数据,求:
的关系如图乙所示,利用图象和题中的已知数据,求: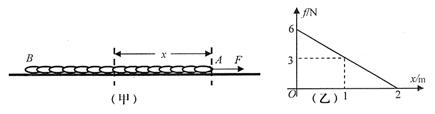
(1)距A端1.5m处绳内的张力多大?
(2)绳子的质量多大?
假期中,小芳乘坐火车外出旅游,当火车在一段平直轨道上匀加速行驶时,她用身边的器材测出火车的加速度。小芳的测量过程如下:她一边看着窗外每隔100m的路标,一边用手表记录着时间。她观测到她所在车厢从经过第一根路标到经过第二根路标的时间为12s,从经过第一根路标到经过第三根路标时间间隔为22s,请你根据她的测量结果,求:
(1)火车的加速度大小?(结果保留三位有效数字)
(2)火车经过第三根路标的速度大小?(结果保留三位有效数字)
(8分) 如图所示,薄板形斜面体竖直固定在水平地面上,其倾角为θ=37°.一个“Π”的物体B紧靠在斜面体上,并可在水平面上自由滑动而不会倾斜,B的质量为M=2kg。一根质量为m=1kg的光滑细圆柱体A搁在B的竖直面和斜面之间。现推动B以水平加速度a=4m/s2向右运动,并带动A沿斜面方向斜向上运动。所有摩擦都不计,且不考虑圆柱体的滚动,g=10m/s2。(sin37°=0.6,cos37°=0.8,)求: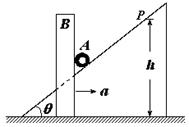
(1)圆柱体A的加速度?
(2)B物体对A的推力F的大小?