如图所示,用与竖直方向成0角的轻绳a和水平轻绳b共同连接一个小球,现保持小球在原位置不动,使绳b在原竖直面内自水平缓慢逆时针方向转动至竖直位置过程中,a绳的拉力变化情况: ( )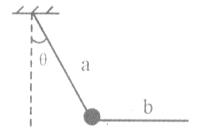
| A.逐渐增大 |
| B.逐渐变小 |
| C.先增大后减小 |
| D.先减小后增大 |
有甲、乙两个小孩站在两辆完全相同的小车上,甲、乙两小孩的质量相等,但甲的力气比乙的力气大,他们各自握紧同一条绳子的两端而用力拉对方.如不考虑地面与车之间的摩擦力,则()
| A.甲车先到达原先两车位置的中央 |
| B.乙车先到达原先两车位置的中央 |
| C.两车同时到达原来两车位置的中央 |
| D.条件不够,无法判断两车谁先到达原来两车位置的中央 |
一辆静止的马车在马的拉力下开始运动,下列说法正确的是()
| A.只会存在马拉车的力,不会存在车拉马的力 |
| B.先有马拉车的力,然后才有车拉马的力 |
| C.马拉车的力大于车拉马的力,所以车向前运动 |
| D.马拉车与车拉马的力同时产生、大小相同、方向相反 |
如图所示,物体A静止放在水平地面上,则()
| A.地面对物体的支持力的大小等于物体的重力,这两个力是一对相互平衡的力 |
| B.物体所受的重力和地面对它的支持力是一对作用力与反作用力 |
| C.物体对地面的压力就是物体的重力,这两个力是同一种性质的力 |
| D.物体对地面的压力和地面对物体的支持力是一对相互平衡的力 |
以下说法错误的是()
A.自由下落的物体因完全失重,所以它对地球没有反作用力
B.两叠放着的木块A、B一起在光滑斜面上自由下滑而没有相对滑动,A、B之间没有摩擦力
C.物体受到一对平衡力作用,撤去其中一个力,另一个力也同时消失
D.作用力和反作用力可以是不同性质的力
两个小球A和B,中间用弹簧连接,并用细绳悬于天花板下,如图所示.下面四对力中属于平衡力的是()
| A.绳对A的拉力和弹簧对A的拉力 | B.弹簧对A的拉力和弹簧对B的拉力 |
| C.弹簧对B的拉力和B对弹簧的拉力 | D.B受的重力和弹簧对B的拉力 |
