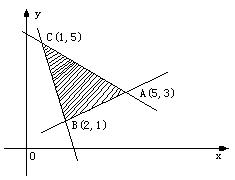
给出平面区域G,如图所示,其中A(5,3),B(2,1),C(1,5)。若使目标函数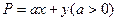 取得最大值的最优解有无穷
取得最大值的最优解有无穷 多个,则
多个,则 的值为( )
的值为( )
| A.4 | B.2 |
C. |
D. |
下列推理是归纳推理的是( )
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜想出椭圆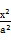 + +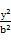 =1的面积S=πab =1的面积S=πab |
| D.以上均不正确 |
设P和Q是两个集合,定义集合P+Q={x|x∈P或x∈Q且x∉P∩Q}.若P={x|x2-3x-4≤0},Q={x|y=log2(x2-2x-15)},那么P+Q等于( )
| A.[-1,4] |
| B.(-∞,-1]∪[4,+∞) |
| C.(-3,5) |
| D.(-∞,-3)∪[-1,4]∪(5,+∞) |
数列{an}满足an+an+1= (n∈N*),a2=2,Sn是数列{an}的前n项和,则S2015为( )
(n∈N*),a2=2,Sn是数列{an}的前n项和,则S2015为( )
| A.502 | B.504 | C.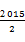 |
D.2015 |
已知函数f(x)是R上的单调增函数且为奇函数,数列{an}是等差数列,a3>0,则f(a1)+f(a3)+f(a5)的值( )
| A.恒为正数 | B.恒为负数 |
| C.恒为0 | D.可以为正数也可以为负数 |
已知函数f(x)满足f(x+1)= +f(x),x∈R,且f(1)=
+f(x),x∈R,且f(1)= ,则数列{f(n)}(n∈N*)的前20项的和为( )
,则数列{f(n)}(n∈N*)的前20项的和为( )
| A.305 | B.315 | C.325 | D.335 |