日本物理学家小林诚和益川敏英由于发现了对称性破缺的起源，并由此预言的六个夸克逐渐被实验证实，获得2008年诺贝尔物理学奖．夸克之间的强相互作用势能可写为
，式中r是正、反顶夸克之间
的距离，as＝0．12是强相互作用耦合系数，k2是与单位制有关的常数，在国际单位制中k2=0．319×10-25J·m；而在电荷之间的相互作用中，相距为r，电荷量分别为q1q2的两个点电荷之间的电势能
，式中k1是静电力常量．根据题中所给信息可以判定下列说法正确的是 （ ）
A．正反顶夸克之间的相互作用力为 |
B．正反顶夸克之间的相互作用力为 |
C．若地球质量为M，则轨道半径为r，质量为m的地球卫星的万有引力势能为 |
D．若地球质量为M，则轨道半径为r、质量为m的地球卫星的万有引力势能为 |
物块从光滑曲面上的P点自由滑下，通过粗糙的静止水平传送带以后落到地面上的Q点，若传送带的皮带轮沿逆时针方向转动起来，使传送带随之运动，如图1－16所示，再把物块放到P点自由滑下则 [ ]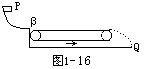 
| A．物块将仍落在Q点 |
| B．物块将会落在Q点的左边 |
| C．物块将会落在Q点的右边 |
| D．物块有可能落不到地面上 |
如图所示，在同一条竖直线上，有电荷量均为Q的A、B两个正点电荷，； GH是它们连线的垂直平分线．另有一个带电小球C，质量为m、电荷量为＋q(可视为点电荷），被长为l的绝缘轻细线悬挂于O点，现在把小球C拉起到M点，使细线水平且与A、B处于同一竖直面内，由静止开始释放，小球C向下运动到GH线上的N点时刚好速度为零，此时细线与竖直方向的夹角
= 300．试求：
(1)在A、B所形成的电场中，M、N两点间的电势差，并指出M、N哪一点的电势高．
(2)若N点与A、B两个点电荷所在位置正好形成一个边长为a的正三角形，则小球运动到N
点瞬间，轻细线对小球的拉力FT（静电力常量为k).
如图，竖直放置的斜面下端与光滑的圆弧轨道BCD的B端相切，圆弧半径为R，∠COB=q，斜面倾角也为q，现有一质量为m的小物体从斜面上的A点无初速滑下，且恰能通过光滑圆形轨道的最高点D.已知小物体与斜面间的动摩擦因数为m，求：（1）AB长度l应该多大。（2）小物体第一次通过C点时对轨道的压力多大。
地球以角速度
绕地轴自转，一只热气球相对地面静止在赤道上空（不计气球离地高度），已知地球半径为R，在距地面h高处的圆形轨道上有一颗人造地球卫星，设地球质量为M，热气球的质量为m，人造地球卫星的质量为m1，根据上述条件，有一位同学列出了以下两个式子：
对热气球有：
（1）
对人造地球卫星有：（2）
进而求出了人造地球卫星绕地球运行的角速度
这两个式子中有一个是错误的，找出来，并说明理由。现补充一个条件：已知第一宇宙速度为v1,求距地h处的人造地球卫星绕地球运行的角速度
一路桥工人在长l=300米的隧道中，突然发现一汽车在离右隧道口s=150米处以速度vo=54千米/小时向隧道驶来，由于隧道内较暗，司机没有发现这名工人。此时路桥工人正好处在向左、向右以某一速度匀速跑动都恰能跑出隧道而脱险的位置。问此位置距右出口距离x是多少?他奔跑的最小速度是多大? 