过抛物线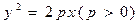 的对称轴上一点
的对称轴上一点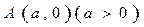 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线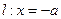 作垂线,垂足分别为
作垂线,垂足分别为 、
、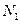 。
。
(Ⅰ)当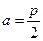 时,求证:
时,求证: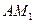 ⊥
⊥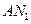 ;
;
(Ⅱ)记
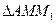 、
、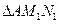 、
、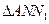 的面积分别为
的面积分别为 、
、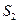 、
、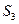 ,是否存在
,是否存在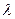 ,使得对任意的
,使得对任意的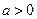 ,都有
,都有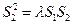 成立。若存在,求
成立。若存在,求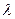 值;若不在,说明理由。
值;若不在,说明理由。
汽车是碳排放量比较大的行业之一.欧盟规定,从2012年开始,将对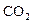 排放量超过
排放量超过 的
的 型新车进行惩罚.某检测单位对甲、乙两类
型新车进行惩罚.某检测单位对甲、乙两类 型品牌车各抽取
型品牌车各抽取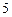 辆进行
辆进行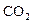 排放量检测,记录如下(单位:
排放量检测,记录如下(单位: ).
).
| 甲 |
80 |
110 |
120 |
140 |
150 |
| 乙 |
100 |
120 |
 |
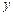 |
160 |
经测算发现,乙品牌车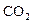 排放量的平均值为
排放量的平均值为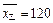
 .
.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆不符合 排放量的概率是多少?
排放量的概率是多少?
(Ⅱ)若 ,试比较甲、乙两类品牌车
,试比较甲、乙两类品牌车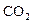 排放量的稳定性.
排放量的稳定性.
已知向量
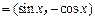 ,
,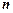
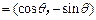 ,其中
,其中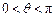 .函数
.函数
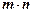 在
在 处取最小值.
处取最小值.
(Ⅰ)求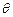 的值;
的值;
(Ⅱ)设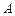 ,
,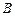 ,
, 为
为 的三个内角,若
的三个内角,若 ,
,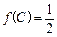 ,求
,求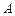 .
.
设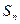 是数列
是数列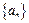 的前
的前 项和,且
项和,且 是
是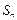 和
和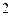 的等差中项.
的等差中项.
(1)求数列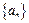 的通项公式;
的通项公式;
(2)当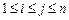 (
(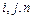 均为正整数)时,求
均为正整数)时,求 和
和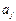 的所有可能的乘积
的所有可能的乘积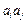 之和
之和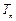 ;
;
(3)设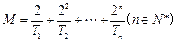 ,求证:
,求证: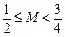 .
.
已知抛物线 :
: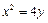 的焦点为
的焦点为 ,过点
,过点 作直线
作直线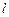 交抛物线
交抛物线 于
于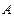 、
、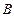 两点;椭圆
两点;椭圆 的中心在原点,焦点在
的中心在原点,焦点在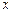 轴上,点
轴上,点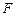 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率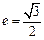 .
.
(1)求椭圆 的方程;
的方程;
(2)经过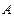 、
、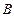 两点分别作抛物线
两点分别作抛物线 的切线
的切线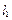 、
、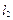 ,切线
,切线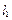 与
与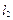 相交于点
相交于点 .证明:
.证明: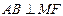 ;
;
(3)椭圆 上是否存在一点
上是否存在一点 ,经过点
,经过点 作抛物线
作抛物线 的两条切线
的两条切线 、
、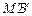 (
( 、
、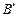 为切点),使得直线
为切点),使得直线 过点
过点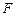 ?若存在,求出抛物线
?若存在,求出抛物线 与切线
与切线 、
、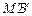 所围成图形的面积;若不存在,试说明理由.
所围成图形的面积;若不存在,试说明理由.
 |
设函数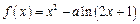 (
(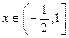 ,
,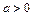 ).
).
(1)若函数 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;
(2)函数 是否有最小值?若有最小值,指出其取得最小值时
是否有最小值?若有最小值,指出其取得最小值时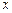 的值,并证明你的结论.
的值,并证明你的结论.