甲乙丙丁四位同学各自对 两变量的线性相关性进行分析,并用回归分析方法得到相关系数
两变量的线性相关性进行分析,并用回归分析方法得到相关系数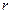 与残差平方和
与残差平方和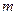 ,如右表则哪位同学的试验结果体现
,如右表则哪位同学的试验结果体现 两变量更强的线性相关性( )
两变量更强的线性相关性( )
| |
甲 |
乙 |
丙 |
丁 |
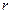 |
 |
 |
 |
 |
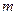 |
 |
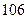 |
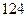 |
 |
A 甲 B 乙 C 丙 D 丁
已知函数 .集合
.集合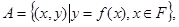
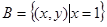 则
则 中所含元素的个数是()
中所含元素的个数是()
| A.0 | B.1 | C.0或1 | D.1或2 |
设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B=()
| A.{1,2} | B.{1,5} | C.{2,5} | D.{1,2,5} |
已知全集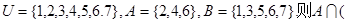
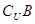 )等于()
)等于()
| A.{2,4,6} | B.{1,3,5} |
| C.{2,4} | D.{2,5} |
如果函数f(x)在[a,b]上是增函数,对于任意的x1,x2∈[a,b](x1≠x2),下列结论不正确的是( )
A.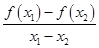 >0 >0 |
| B.f(a)<f(x1)<f(x2)<f(b) |
| C.(x1-x2) [f(x1)-f(x2)]>0 |
D.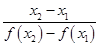 >0 >0 |
若函数f(x)=4x2-kx-8在[5,8]上是单调函数,则k的取值范围是( )
| A.(-∞,40] | B.[40,64] |
| C.(-∞,40]∪[64,+∞) | D.[64,+∞) |