某一星球的第一宇宙速度为v,质最为m的宇航员在这个星球表面受到的重力为W,
万有引力恒量为G,则这个星球
A.半径为 |
B.质量为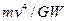 |
C.半径为 |
D.质量为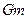 |
物理学家通过艰辛的实验和理论研究探究自然规律,为人类的科学做出了巨大贡献,值得我们敬仰。下列描述中符合物理学史实的是:()
| A.麦克斯韦建立了完整的电磁场理论,并预言电磁波的存在; |
| B.开普勒发现了行星运动三定律,从而提出了日心学说 |
| C.奥斯特发现了电流的磁效应并提出了分子电流假说 |
| D.法拉第发现了电磁感应现象并总结出了判断感应电流方向的规律 |
(多选题,4分)学习物理除了知识的学习外,还要领悟并掌握处理物理问题的思想与方法,如图所示是高中阶段观察或操作过的几个实验,其中研究物理问题的思想方法相同的是()
| A.⑴⑵ | B.⑵⑶ | C.⑶⑷ | D.⑴⑷ |
在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器。闭合电键S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表的示数随电路中电流变化的完整过程图线如图(b)所示。则 ( )
| A.图线甲是电压表V2示数随电流变化的图线 |
| B.电源内电阻的阻值为10Ω |
| C.电源的最大输出功率为3.6W |
| D.滑动变阻器R2的最大功率为0.9W |
如图所示,波源S1在绳的左端发出频率为f1、振幅为A1=2A的半个波形a,同时另一个波源S2在绳的右端发出频率为f2、振幅为A2=A的半个波形b,f2=2f1,P为两个波源连线的中点,则下列说法中正确的有()
| A.两列波同时到达P点 |
| B.两个波源的起振方向相同 |
| C.两列波在P点叠加时P点的位移最大可达3A |
| D.两列波相遇时,绳上位移可达3A的点只有一个,此点在P点的左侧 |
如图所示,在两等量异种点电荷的电场中,MN为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a与c关于MN对称,b点位于MN上,d点位于两电荷的连线上。以下判断正确的是()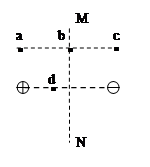
| A.b点场强大于d点场强 |
| B.b点场强小于d点场强 |
| C.a、b两点的电势差等于b、c两点间的电势差 |
| D.试探电荷+q在a点的电势能小于在c点的电势能 |