（本题8分））要求摩托车由静止开始在尽量短的时间内走完一段直道，然后驶入一段半圆形的弯道，但在弯道上行驶时车速不能太快，以免因离心作用而偏出车道．求摩托车在直道上行驶所用的最短时间．有关数据见表格．
某同学是这样解的：要使摩托车所用时间最短，应先由静止加速到最大速度 V1＝40 m/s，然后再减速到V2＝20 m/s，1=v1/a1 …； t2=（v1-v2）/a2 …； t= t1 + t2
你认为这位同学的解法是否合理？若合理，请完成计算；若不合理，请说明理由，并用你自己的方法算出正确结果．
航天飞机是一种垂直起飞、水平降落的载人航天器。航天飞机降落在平直跑道上，其减速过程可简化为两个匀减速直线运动。航天飞机以水平速度v0着陆后立即打开减速阻力伞（如图），加速度大小为a1，运动一段时间后速度减为v；随后在无阻力伞情况下匀减速直至停下，已知两个减速滑行总时间为t。求：
（1）第二个减速阶段航天飞机运动的加速度大小；
（2）航天飞机着陆后滑行的总路程。
如图所示，两光滑金属导轨，间距d="0.2" m，在桌面上的部分是水平的，处在磁感应强度B="0.1" T、方向竖直向下的有界磁场中，电阻R="3" Ω，桌面高H="0.8" m，金属杆ab质量m="0.2" kg、电阻r="1" Ω，在导轨上距桌面h="0.2" m高处由静止释放，落地点距桌面左边缘的水平距离s="0.4" m，g="10" m/s2，求：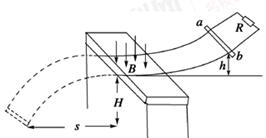
（1）金属杆刚进入磁场时，R上的电流大小；
（2）整个过程中R放出的热量．
如图所示，圆柱体汽缸倒置在水平地面上，汽缸内部封闭有一定质量空气，汽缸质量M=10kg，缸壁厚度忽略不计，活塞质量m=5kg，其横截面积S=50cm2，活塞与缸壁的摩擦不计。在缸内气体的温度为27℃时，活塞刚好与地面相接触，但对地面无压力。现在对汽缸传热，使缸内气体温度上升，求当汽缸对地面刚好无压力时，缸内气体温度是多少摄氏度？（大气压强p0=1.0×105Pa，g取10N/kg）
一小型水电站，其交流发电机的输出功率为1 000 kW，输出电压为1 000 V，在输电过程中，要求输电线能量损耗不大于4%，已知输电线电阻为16 Ω，用户降压变压器的输出电压为240 V，求输电线路中升压变压器与降压变压器的变压比各多大？
交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动．一小型发电机的线圈共220匝，线圈面积S＝0.05 m2，线圈转动的频率为50 Hz，线圈内阻不计，磁场的磁感应强度B＝
T．如果用此发电机带动两个标有“220 V，11 kW”的电机正常工作，需在发电机的输出端a、b与电机之间接一个理想变压器，电路如图所示．求：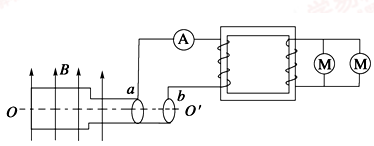
（1）发电机的输出电压为多少？
（2）变压器原、副线圈的匝数比为多少？
（3）与变压器原线圈串联的交流电流表的示数为多少？