（选修3—3模块）
（1）以下说法中正确的是
| A．被活塞封闭在空缸中的一定质量的理想气体，若体积不变，压强增大，则气缸在单位面积上，单位时间内受到的分子碰撞次数增加 |
| B．布朗运动是悬浮在液体中固体颗粒的分子无规则运动的反映 |
| C．分子间距增大，分子势能就一定增大 |
| D．用力拉铁棒的两端，铁棒没有断，这是分子间存在吸引力的宏观表现 |
（2）如图所示，气缸内封闭一定质量的某种理想气体，活塞通过滑轮和一重物连接并保持平衡，已知活塞距缸口0.2m，活塞面积10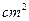
，大气压强
，物重50N，活塞质量及一切摩擦不计，缓慢升高环境温度，使活塞刚好升到缸口，封闭气体吸收了60J的热量，则封闭气体的压强将 （选填“增加”、“减小”或“不变”），气体内能变化量为 J。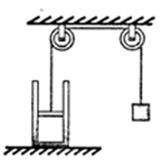
（3）一滴体积为V的油酸，配制成体积比为1：k的油酸溶液（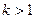
），现取一滴体积仍为V的油酸溶液在滴在水面上，在水面上形成面积为S的单分子油膜，已知油酸的密度为
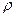，摩尔质量为M。请据此推算阿伏伽德罗常数的表达式。
一辆电动自行车的铭牌上给出了如下的技术参数表。
| 规格 |
后轮驱动直流电机 |
||
| 车型 |
26英寸 |
额定输出功率 |
120W |
| 整车质量 |
30kg |
额定电压 |
40V |
| 最大载量 |
120kg |
额定电流 |
4.0A |
请根据上表计算
（1）此车电机的内阻；
（2）电机正常工作时的效率；
（3）在额定电压下，电机突然卡死时，电机的总功率。
用油膜法可粗略测出阿伏加德罗常数，把密度ρ=0.8×103 kg/m3的某种油，用滴管滴出一滴油在水面上形成油膜，已知这滴油的体积V=0.5×10-3 cm3，形成的油膜的面积S="0.7" m2，油的摩尔质量Ml="0.09" kg/mol.若把油膜看成单分子层，每个油分子看成球形，那么：
（1）油分子的直径为多大？
（2）由以上数据可测出的阿伏加德罗常数大约为多少？（保留一位有效数字）
将1 cm3油酸溶于酒精，制成200 cm3的酒精油酸溶液.已知1 cm3溶液有50滴，现取1滴溶液滴到水面上，随着酒精溶于水，油酸在水面上形成一单分子薄层，已测出这一薄层的面积为0.2 m2，由此估算油酸分子直径.
某种油的密度ρ=0.8×103 kg/m3，把一滴体积为1.2×10-3 cm3的这种油滴在水面上，可以形成面积为2 m2的单分子油膜，阿伏加德罗常数NA=6.02×1023 mol-1.若把分子看作球形，则估算出它的直径是多大？油的摩尔质量是多少？
如图所示，A、B是竖直放置的中心带有小孔的平行金属板，两板间的电压为U1=100V，C、D是水平放置的平行金属板，板间距离为d=0.2m，板的长度为L=1m，P是C板的中点，A、B两板小孔连线的延长线与C、D两板的距离相等，将一个负离子从板的小孔处由静止释放，求：
（1）为了使负离子能打在P点，C、D两板间的电压应为多少？哪板电势高？
（2）如果C、D两板间所加的电压为2V，则负离子能打在板上吗？若不能打在板上，它离开电场时发生的侧位移多少？