（本小题满分13分）
已知椭圆E的中心在坐标原点，焦点在x轴上，离心率为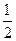
，且椭圆E上一点到两个焦点距离之和为4；
是过点P（0，2）且互相垂直的两条直线，
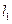交E于A，B两点，
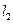交E交C，D两点，AB，CD的中点分别为M，N。
（1）求椭圆E的方程；
（2）求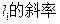
k的取值范围；
（3）求
的取值范围。
的偶函数，其图象关于点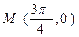
对称，且在区间
上是单调
函数.求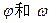
的值.
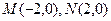已知两点
，点
为坐标平面内的动点，且满足
.
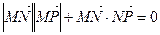(Ⅰ)求点的轨迹
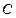的方程;
(Ⅱ)设过点
的直线
斜率为
，且与曲线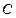相交于点
、
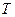，若、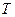两点只在第二象限内运动，线段
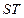的垂直平分线交
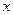轴于
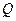点，求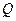点横坐标的取值范围.
已知函数
，直线
与函数
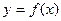图象相切.
（Ⅰ）求直线的斜率
的取值范围；
（Ⅱ）设函数
，已知函数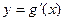
的图象经过点
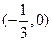，求函数
的极值.
从7个不同的红球，3个不同的白球中取出4个球，问：
（1）一共有多少种不同的取法？
（2）其中恰有一个白球的取法有多少种？
（3）其中至少有两个白球的取法有多少种？
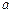
⑴当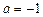
时，求函数
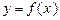的值域；
⑵若函数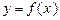在定义域上是减函数，求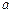的取值范围；
⑶求函数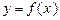在x∈(0，1]上的最大值及最小值，并求出函数取最值时
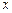的值