甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为a，再由乙猜甲刚才想的数字，把乙猜的数字记为b,且a,b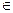 
{1，2，3，4},若|a
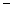b| 
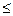1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 （分式表示）
i是虚数单位，复数z=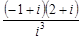
的虚部为_________.
已知曲线C的极坐标方程是
．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：
（
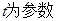），则直线l与曲线C相交所成的弦的弦长为______．
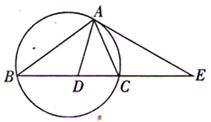
如图，
的外接圆的切线
与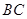
的延长线相交于点
，
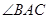的平分线与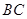相交于点
，若
，
，则
______．
科拉茨是德国数学家，他在1937年提出了一个著名的猜想：任给一个正整数n,如果n是偶数，就将它减半（即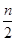
）；如果n是奇数，则将它乘3加1（即
），不断重复这样的运算，经过有限步后，一定可以得到1．如初始正整数为6，按照上述变换规则，我们可以得到一个数列：6，3，10，5，16，8，4，2，1．对于科拉茨猜想，目前谁也不能证明，也不能否定，现在请你研究：
（1）如果
，则按照上述规则施行变换后的第8项为．
（2）如果对正整数
（首项）按照上述规则施行变换后的第8项为1（注：1可以多次出现），则的所有不同值的个数为．
若函数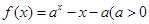
且
有两个零点，则实数
的取值范围是．