(本小题满分14分)已知平面向量
=(
，－1)，
=(x，y)(x>0)，
=1．
(Ⅰ)若对任意实数t都有
,求向量；
(Ⅱ)令
=
+(sin2α－2cos2α)，
=(
sin22α)+(cos2α)，α∈(
，π)，若⊥，
，求tanα的值；
(Ⅲ)在(Ⅱ)的条件下，求
的值．
平面内有一长度为2的线段AB和一动点P，若满足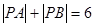
，
则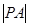
的取值范围是：（）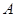
设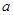
是甲抛掷一枚骰子（六个面分别标有1－6个点的正方体）得到的点数，则方程
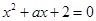有两个不相等的实数根的概率为（）
A． |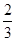
B． |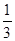
C． |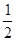
D． |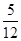
已知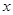
与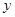
之间的一组数据如图所示，则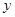与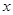的线性回归方程
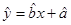必过点（ )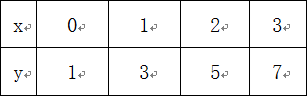 
| A．(1, 2) | B．（2，2） | C．（1.5，0） | D．（1.5，4） |
若右图所示程序执行的结果是5，则输入的x值是（）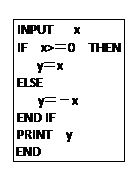
| A．5 | B．-5 | C．5或-5 | D．不能确定 |
有20位同学，编号从1至20，现在从中抽取4人作问卷调查，用系统抽样方法确定所抽的编号可能为( )
| A．5，10，15，20 | B．2，6，10，14 |
| C．2，4，6，8 | D．5，8，11，14 |