(在十字路口,汽车以 的加速度从停车线启动做匀加速运动,恰好有一辆自行车以
的加速度从停车线启动做匀加速运动,恰好有一辆自行车以 的速度匀速驶过停车线与汽车同方向行驶,求:
的速度匀速驶过停车线与汽车同方向行驶,求:
(1) 什么时候它们相距最远?最远距离是多少?
(2) 在什么地方汽车追上自行车?追到时汽车的速度是多大?
如图所示:在真空中,有一半径为r的圆形区域内充满垂直纸面向里的匀强磁场,磁感应强度为B,一带电粒子质量为m,电量为q,以某一速度由a点沿半径方向射入磁场,从c点射出磁场时其速度方向改变了60度,(粒子的重力可忽略)试求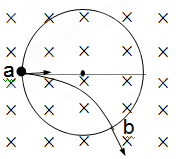
(1)该粒子在磁场中运动时间t
(2)粒子做圆周运动的半径R
(3)粒子运动的速度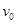
如图所示电路中,R1=0.8Ω,R3=6Ω,滑动变阻器的全值电阻R2="12" Ω,电源电动势E="6" V,内阻r="0.2" Ω,当滑动变阻器的滑片在变阻器中央位置时,闭合开关S,电路中的电流表和电压表的读数各是多少?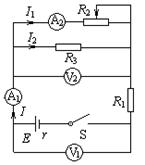
如右图所示,在某空间实验室中,有两个靠在一起的等大的圆柱形区域,分别存在着等大反向的匀强磁场,磁感应强度B=0.10 T,磁场区域半径r=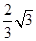 m,左侧区圆心为O1,磁场向里,右侧区圆心为O2,磁场向外.两区域切点为C.今有质量m=3.2×10-26 kg.带电荷量q=1.6×10-19 C的某种离子,从左侧区边缘的A点以速度v=106 m/s正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区穿出.求:
m,左侧区圆心为O1,磁场向里,右侧区圆心为O2,磁场向外.两区域切点为C.今有质量m=3.2×10-26 kg.带电荷量q=1.6×10-19 C的某种离子,从左侧区边缘的A点以速度v=106 m/s正对O1的方向垂直磁场射入,它将穿越C点后再从右侧区穿出.求:
(1)该离子通过两磁场区域所用的时间.
(2)离子离开右侧区域的出射点偏离最初入射方向的侧移距离为多大?(侧移距离指垂直初速度方向上移动的距离)
如图所示,真空中有以O′为圆心,r为半径的圆柱形匀强磁场区域,圆的最下端与x轴相切于坐标原点O,圆的右端与平行于y轴的虚线MN相切,磁感应强度为B,方向垂直纸面向外,在虚线MN右侧x轴上方足够大的范围内有方向竖直向下、场强大小为E的匀强电场.现从坐标原点O向纸面内不同方向发射速率相同的质子,质子在磁场中做匀速圆周运动的半径也为r,已知质子的电荷量为e,质量为m,不计质子的重力、质子对电磁场的影响及质子间的相互作用力.求:
(1)质子进入磁场时的速度大小;
(2)沿y轴正方向射入磁场的质子到达x轴所需的时间.
11.(18分)如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应为B,方向垂直xOy平面向里,电场线平行于y轴。一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴的方向夹角为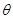 .不计空气阻力,重力加速度为g,求
.不计空气阻力,重力加速度为g,求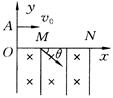
(1)电场强度E的大小和方向;
(2)小球从A点抛出时初速度v0的大小;
(3)A点到x轴的高度h.