已知函数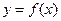 是
是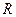 上的偶函数,对任意
上的偶函数,对任意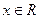 ,都有
,都有 成立,当
成立,当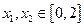 且
且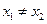 时,都有
时,都有 给出下列命题:
给出下列命题:
①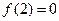 且
且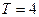 是函数
是函数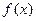 的一个周期;②直线
的一个周期;②直线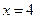 是函数
是函数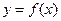 的一条对称轴;③函数
的一条对称轴;③函数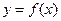 在
在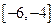 上是增函数;④函数
上是增函数;④函数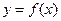 在
在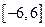 上有四个零点.其中正确命题的序号为___________(把所有正确命题的序号都填上)
上有四个零点.其中正确命题的序号为___________(把所有正确命题的序号都填上)
已知圆C的参数方程为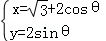 (θ为参数),若P是圆C与y轴正半轴的交点,以原点为极点,x轴的正半轴为极轴建立极坐标系,求过点P的圆C的切线的极坐标方程.
(θ为参数),若P是圆C与y轴正半轴的交点,以原点为极点,x轴的正半轴为极轴建立极坐标系,求过点P的圆C的切线的极坐标方程.
如图,一个底面半径为R的圆柱被与其底面所成角为θ(0°<θ<90°)的平面所截,截面是一个椭圆,
当θ为30°时,这个椭圆的离心率为.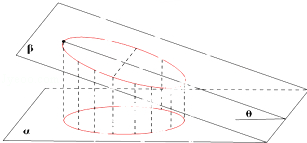
在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为.
一只半径为R的球放在桌面上,桌面上一点A的正上方相距(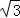 +1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为.
+1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为.
底面直径为10的圆柱被与底面成60°的平面所截,截口是一个椭圆,该椭圆的长轴长,短轴长,离心率为.