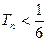已知椭圆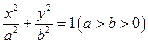 的离心率
的离心率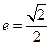 ,短轴长为
,短轴长为 .
.
(Ⅰ)求椭圆方程;(Ⅱ)若椭圆与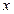 轴正半轴、
轴正半轴、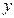 轴正半轴的交点分别为
轴正半轴的交点分别为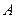 、
、 ,经过点
,经过点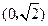 且斜率为
且斜率为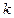 的直线
的直线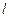 与椭圆交于不同的两点
与椭圆交于不同的两点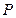 、
、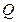 .是否存在常数
.是否存在常数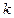 ,使得向量
,使得向量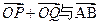 共线?如果存在,求
共线?如果存在,求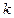 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(本小题满分12分)
一个口袋中装有大小相同的2个白球和3个黑球.
(1)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的分布列与期望。
(本小题满分 分)
分)
设三角形 的内角
的内角 的对边分别为
的对边分别为
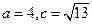 ,
,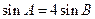 .
.
(1)求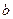 边的长;
边的长;
(2)求角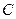 的大小;
的大小;
(3)求三角形 的面积
的面积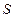 。
。
(本小题满分12分)已知二次函数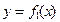 的
的 图象以原点为顶点且过点(1,1),反比例函数
图象以原点为顶点且过点(1,1),反比例函数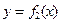 的图象与直线
的图象与直线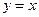 的两个交点间的距离为8,
的两个交点间的距离为8,
(1)求函数 的表达式;
的表达式;
(2)证明:当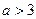 时,关于
时,关于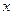 的方程
的方程 有三个实数解.
有三个实数解.
(本小题满分12分)如图5, 中,
中,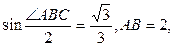
点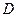 在线
在线 段
段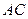 上,且
上,且 ,
,
(Ⅰ)求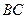 的长;
的长;
(Ⅱ)求 的面积.
的面积.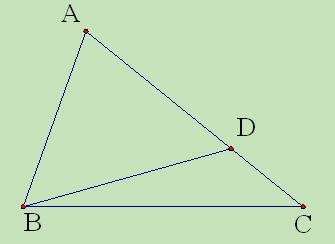
(本小题满分12分)已知数列
(1)求数列{ }的通项公式。
}的通项公式。
(2)设数列 ,数列{
,数列{ }的前n项和为
}的前n项和为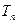 ,证明
,证明