(本小题满分14分)
已知函数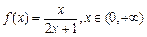 ,数列
,数列 满足
满足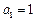 ,
,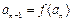 ;数列
;数列 满足
满足 ,
,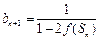 ,其中
,其中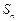 为数列
为数列 前几项和,
前几项和,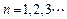
(1)求数列 和数列
和数列 的通项公式;
的通项公式;
(2)设 ,证明
,证明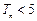 .
.
已知函数f(x)=lnx,g(x)=k·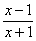 .
.
(I)求函数F(x)= f(x)- g(x)的单调区间;
(Ⅱ)当x>1时,函数f(x)> g(x)恒成立,求实数k的取值范围;
(Ⅲ)设正实数a1,a2,a3,,an满足a1+a2+a3++an=1,
求证:ln(1+ )+ln(1+
)+ln(1+ )++ln(1+
)++ln(1+ )>
)> .
.
数列{an}是公比为 的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n
的等比数列,且1-a2是a1与1+a3的等比中项,前n项和为Sn;数列{bn}是等差数列,b1=8,其前n项和Tn满足Tn=n ·bn+1(
·bn+1( 为常数,且
为常数,且 ≠1).
≠1).
(I)求数列{an}的通项公式及 的值;
的值;
(Ⅱ)比较 +
+ +
+ ++
++ 与了
与了 Sn的大小.
Sn的大小.
已知向量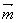 =(
=(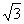 sin2x+2,cosx),
sin2x+2,cosx),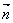 =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)= 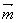 ·
·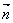 .
.
(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若a=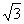 ,f(A)=4,求b+c的最大值.
,f(A)=4,求b+c的最大值.
在矩形ABCD中,|AB|=2 ,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且 =
=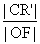 =
= .
.
(Ⅰ)求证:直线ER与GR′的交点P在椭圆 :
: +
+ =1上;
=1上;
(Ⅱ)若M、N为椭圆 上的两点,且直线GM与直线GN的斜率之积为
上的两点,且直线GM与直线GN的斜率之积为 ,求证:直线MN过定点;并求△GMN面积的最大值.
,求证:直线MN过定点;并求△GMN面积的最大值.
2013年2月20日,针对房价过高,国务院常务会议确定五条措施(简称“国五条”).为此,记者对某城市的工薪阶层关于“国五条”态度进行了调查,随机抽取了60人,作出了他们的月收入的频率分布直方图(如图),同时得到了他们的月收入情况与“国五条”赞成人数统计表(如下表):
| 月收入(百元) |
赞成人数 |
| [15,25) |
8 |
| [25,35) |
7 |
| [35,45) |
10 |
| [45,55) |
6 |
| [55,65) |
2 |
| [65,75) |
1 |
(I)试根据频率分布直方图估计这60人的平均月收入;
(Ⅱ)若从月收入(单位:百元)在[15,25),[25,35)的被调查者中各随机选取3人进行追踪调查,记选中的6人中不赞成“国五条”的人数为X,求随机变量X的分布列及数学期望.