如图,把一带正电的小球a放在光滑绝缘面上,欲使球a能静止在斜面上,需在MN间放一带电小球b,则b应( )
| A.带正电,放在A点 |
| B.带正电,放在B点 |
| C.带负电,放在C点 |
| D.带正电,放在C点 |
在光滑斜面顶端释放一物体,物体做初速为0的匀加速直线运动,把斜面分成距离相等的三段,按从上到下的顺序,通过这三段连续的位移所需的时间之比是
| A.1:2:3 | B.1:4:9 |
C.1: : : |
D.1: : : |
有两个大小相等的共点力F1和F2,当它们的夹角为90°时,合力为F,则当它们间的夹角为60°时,合力的大小为
| A.2F | B. |
C.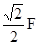 |
D. |
质点做直线运动的v-t图象如图所示,表示质点做匀速直线运动的是
物体做匀加速直线运动,加速度为2m/s2,那么
| A.物体的末速度一定比初速度大2m/s |
| B.每秒钟物体的速度增加2m/s |
| C.第3秒初的速度比第2秒末的速度大2m/S |
| D.第3秒末的速度比第2秒初的速度大2m/s |
如图所示,在工地上,用皮带运输机运送货物,下列说法中正确的是
| A.把货物匀速向高处输送的过程中,货物没有受到摩擦力 |
| B.把货物匀速向高处输送的过程中,货物受到平行于传送带向上的摩擦力 |
| C.把货物匀速向低处输送的过程中,货物没有受到摩擦力 |
| D.把货物匀速向低处输送的过程中,货物受到平行于传送带向下的摩擦力 |