物体在恒定的合力作用下做直线运动,在时间△t1内动能由零增大到E1,在时间△t2内动能由E1增大到2E1. 设合力在△t1内做的功是W1,冲量是I1;在△t2内做的功是W2,冲量I2,那么( )
A.I1<I2,W1=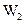 |
B.I1>I2,W1=W2 |
| C.I1<I2,W1<W2 | D.I1=I2,W1<W2 |
如图所示,具有一定质量的小球A固定在轻杆一端,另一端挂在小车支架的O点。用手将小球拉至水平,此时小车静止于光滑水平面上,放手让小球摆下与B处固定的橡皮泥碰击后粘在一起,则在此过程中小车将()
| A.向右运动 |
| B.向左运动 |
| C.静止不动 |
| D.车向左运动后又静止 |
下列关于光电效应的陈述,哪些正确。( )
| A.金属的逸出功与入射光的频率成正比 |
| B.光电流强度与入射光强度无关 |
| C.用不可见光照射金属一定比用可见光照同种金属产生的光电子的初动能大 |
| D.对任何一种金属,都有一个“最大波长”,入射光的波长必须小于这个波长才能产生光电效应 |
在双缝干涉实验中,明暗条纹形成的原因解释正确的是 ( )
| A.暗条纹处一定没有光子到达 |
| B.暗条纹处可能也有光子到达 |
| C.光子到达暗条纹处的概率很小 |
| D.光子到达明条纹处的概率很大 |
爱因斯坦由光电效应的实验规律,猜测光具有粒子性,从而提出光子说,这属于( )
| A.等效替代 | B.控制变量 | C.科学假说 | D.数学归纳 |
如图所示,p、p,分别表示物体受到冲量前、后的动量,短线表示的动量大小为15kg·m/s,长线表示的动量大小为30kg·m/s,箭头表示动量的方向.在下列所给的四种情况下,物体动量改变量相同的是 ()
| A.①② | B.②④ | C.①③ | D.③④ |