(本小题满分10分)

袋中有大小、形状相同的白、黑球各一个,现有放回地随机摸取3次,每次摸取一个球.
(Ⅰ)试问:一共有多少种不同的结果?请列出所有可能的结果; 

(Ⅱ)若摸到白球时得1分,摸到黑球时得2分,求3次摸球所得总分大于4分的概率.
某巡逻艇在A处发现在北偏东 距A处8处有一走私船,正沿东偏南
距A处8处有一走私船,正沿东偏南 的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以
的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以 海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇航行方向。
海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇航行方向。
(3)(本小题满分7分)选修4—5:不等式选讲
已知函数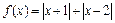 ,不等式
,不等式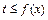 在
在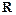 上恒成立.
上恒成立.
(Ⅰ)求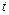 的取
的取 值范围;
值范围;
(Ⅱ)记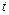
 的最大值为
的最大值为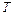 ,若正实数
,若正实数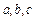 满足
满足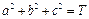 ,求
,求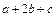 的最大值.
的最大值.
(2)(本小题满分7分)选修4—4:坐标系与参数方程
在直角坐标系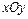 中,曲线
中,曲线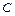 的参数方程为
的参数方程为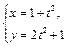 (
(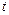 为参数),若圆
为参数),若圆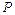 在以该直
在以该直 角坐标系的原点
角坐标系的原点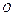 为极点、
为极点、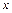 轴的正半轴为极轴的极坐标系下的方程为
轴的正半轴为极轴的极坐标系下的方程为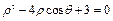
 .
.
(Ⅰ)求曲线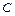 的普通方程和圆
的普通方程和圆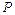 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点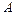 是曲线
是曲线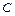 上的动点,点
上的动点,点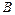 是圆
是圆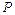 上的动点,求
上的动点,求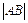 的最小值.
的最小值.
(1)(本小题满分7分)选修4—2:矩阵与变换
已知二阶矩阵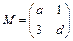 有特征值
有特征值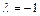 及对应的一个特征向量
及对应的一个特征向量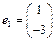 .
.
(Ⅰ)求矩阵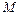 ;
;
(Ⅱ)设曲线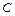 在矩阵
在矩阵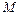 的作用下得到的方程为
的作用下得到的方程为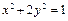 ,求曲线
,求曲线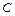 的方程.
的方程.
(本小题满分14分)
已知函数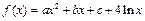 的极值点为
的极值点为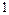 和
和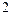 .
.
(Ⅰ)求实数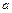 ,
,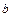 的值;
的值;
(Ⅱ)试讨论方程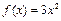 根的个数;
根的个数;
(Ⅲ)设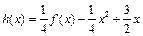 ,斜率为
,斜率为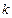 的直线与曲线
的直线与曲线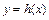 交于
交于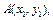
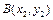
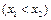 两点,试比较
两点,试比较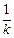 与
与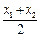 的大小,并给予证明.
的大小,并给予证明.