船在400米宽的河中横渡,河水流速是2m/s,船在静水中的航速是4m/s,试求:
(1)要使船到达对岸的时间最短,船头应指向何处?最短时间是多少?航程是多少?
(2)要使船航程最短,船头应指向何处?最短航程为多少?渡河时间又是多少?
风筝(图甲)借助于均匀的风对其作用力和牵线对其拉力的作用,才得以在空中处于平衡状态.如图乙所示,风筝平面AB与地面夹角为30°,风筝质量为300g,求风对风筝的作用力的大小.(风对风筝的作用力与风筝平面相垂直,g取10m/s2)
图中物块A重10N,A和桌面间的动摩擦因数μ=0.25,当悬挂物B重3N时,开始沿桌面滑动.求: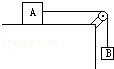
(1)B物体重1N时,A与桌面间的摩擦力多大?
(2)B物体重6N时,A与桌面的摩擦力多大?
(3)当A物体上再加上重10N的C物体,B物体重6N时,A与桌面的摩擦力多大?
一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m1和 m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°.求两小球的质量之比 .
.
某汽车做匀变速直线运动,10s速度从5m/s增加到25m/s,
(1)求汽车在这段运动中的加速度大小?
(2)如果遇到紧急情况刹车,2s内速度由25m/s减到15m/s,这个过程也是匀变速直线运动,求刹车过程中的速度的大小和方向?
(3)刹车后6s末的速度为多少?
以V0=12m∕s的初速度竖直向上抛出一质量为0.5kg的物体,g取10m/s2.
求:不考虑空气阻力,小球上升的最大高度和回到抛出点的时间?