( 20 分)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,运动到最高点时与静止悬挂在此处的小球B发生弹性碰撞(碰撞过程无动能损失),碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O/与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
(1)球B在两球碰撞后一瞬间的速度大小;
(2)球A在两球碰撞前一瞬间的速度大小;
(3)弹簧的弹性力对球A所做的功。
一个质量m=" 6" kg的物体,受到水平方向的拉力F=10N,如图所示,从静止开始在水平地面上移动的距离s= 2m,物体与地面间的滑动摩擦力f= 4N,求: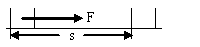
(1)拉力和摩擦力对物体所做的功;
(2)合外力对物体所做的功;
(3)在此过程中物体获得的速度大小。
把一个小球从离地面h=20m处,以v=10m/s的初速度水平抛出,不计空气阻力,求:
(1)小球在空中的飞行时间t ( g=10m/s2 )
(2)小球落地点离抛出点的水平距离s
一辆汽车从静止开始做匀加速直线运动,加速度大小a=3m/s2,求经过10 s后汽车速度的大小?在这段时间里汽车运动了多远?
如图所示,斜面轨道AB与水平面之间的夹角θ=53O,BD为半径R =" 4" m的圆弧形轨道,且B点与D点在同一水平面上,在B点,轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处的一质量m=1kg的小球由静止滑下,经过B、C点后从D点斜抛出去,最后落在地面上的S点处时的速度大小vS= 8m/s,已知A点距地面的高度H = 10m,B点距地面的高度h ="5" m,设以MDN为分界线,其左边为一阻力场区域,右边为真空区域,g取10m/s2, ,
,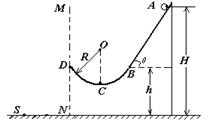
(1)小球经过B点的速度为多大?
(2)小球经过圆弧轨道最低处C点时对轨道的压力多大?
(3)小球从D点抛出后,受到的阻力f与其瞬时速度方向始终相反,求小球从D点至S点的过程中,阻力f所做的功.在此过程中小球的运动轨迹是抛物线吗?
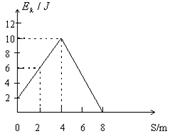
质量M=1kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,运动到位移是8m时物体停止,运动过程中 -S的图线如图所示。求:
-S的图线如图所示。求:
(1)物体的初速度多大?
(2)物体和平面间的摩擦系数为多大?
(3) 拉力F的大小?(g取 )
)