如图所示,条形区域Ⅰ和Ⅱ内分别存在方向垂直于纸面向外和向里的匀强磁场,磁感应强度B的大小均为0.3T,AA′、BB′、CC′、DD′为磁场边界,它们相互平行,条形区域的长度足够长,磁场宽度及BB′、CC′之间的距离d=1m。一束带正电的某种粒子从AA′上的O点以沿与AA′成60°角、大小不同的速度射入磁场,当粒子的速度小于某一值v0时,粒子在区域Ⅰ内的运动时间t0=4×10-6s;当粒子速度为v1时,刚好垂直边界BB′射出区域Ⅰ。取π≈3,不计粒子所受重力。求:
(1)粒子的比荷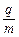 ;
;
(2)速度v0和v1 的大小;
(3)速度为v1的粒子从O到DD′所用的时间。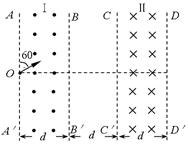
将金属块m用压缩的轻弹簧卡在一个矩形的箱中,如图所示,在箱的上顶板和下底板装有压力传感器,箱可以沿竖直轨道运动。当箱以a=2.0m/s2的加速度竖直向上做匀减速运动时,上顶板的传感器显示的压力为6.0N,下底板的传感器显示的压力为10.0N。(取g=10m/s2)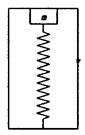
求金属块的质量;
若上顶板传感器的示数变为下底板传感器的示数的一半,请判断箱的运动情况;
若上顶板传感器的示数变为零,请判断箱的运动情况。
人类受飞鸟在空中飞翔的启发而发明了飞机,飞鸟扇动翅膀获得向上的举力可表示为F=kSv2,式中S为翅膀的面积,v为飞鸟的飞行速度,k为比例系数。只有当飞鸟的速度足够大时,飞鸟的举力至少等于它的重力时,飞鸟才能起飞。一个质量为m=0.1kg、翅膀面积为S1的燕子,其最小的飞行速度为v1=10m/s。假设飞机飞行时获得的向上举力与飞鸟飞行时获得的举力有同样的规律,一架质量为M=7200kg,机翼的面积S2为燕子翅膀面积S1的2000倍的飞机,以a=2m/s2的加速度由静止开始加速,则飞机在跑道上滑行多远才能起飞?
为了安全,在公路上行驶的汽车之间应保持必要的距离。已知某高速公路的最高限速v=120km/h。假设前方车辆突然停止,后车司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s。刹车时汽车受到阻力的大小f为汽车重力的0.40倍。该高速公路上汽车间的距离s至少应为多少?
以36km/h速度行驶的列车开始下坡,在坡路上的加速度等于0.2m/s2,经过30s到达坡底,求坡路的长度和列车到达坡底时的速度。
一足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场,矩形区域的左边界ad长为L,现从ad中点O垂直于磁场射入一速度方向与ad边夹角为30°、大小为v0的带正电粒子,如下图所示.已知粒子电荷量为q,质量为m(重力不计):
若要求粒子能从ab边射出磁场,v0应满足什么条件?
若要求粒子在磁场中运动的时间最长,粒子应从哪一条边界处射出,出射点位于该边界上何处?最长时间是多少?